2. 如图,$AD \perp CD$,$AB = 10$,$BC = 20$,$\angle A = \angle C = 30^{\circ}$,则$AD$的长为

5$\sqrt{3}$ + 10
,$CD$的长为10$\sqrt{3}$ + 5
.
答案:$5\sqrt 3+10$
$10\sqrt 3+5$
$10\sqrt 3+5$
3. 如图,两堵墙之间有一架底端在点$A$的梯子,当它靠在一侧墙上时,梯子的顶端在点$B$;当它靠在另一侧墙上时,梯子的顶端在点$D$.已知$\angle BAC = 60^{\circ}$,$\angle DAE = 45^{\circ}$,$DE = 3\sqrt{2}\ m$,则点$B$到地面的距离$BC =$

3$\sqrt{3}$
$ m$.
答案:$3\sqrt 3$
4. 如图,在$\triangle ABC$中,$AD$是边$BC$上的高,$\angle C = 45^{\circ}$,$\sin B = \frac{1}{3}$,$AD = 1$.求$BC$的长.


答案:解:∵∠C=45°
∴CD=AD=1
$AB=\frac {AD}{sinB}=3,$$BD=\sqrt{AB²-AD²}= 2\sqrt{2},$
∴$BC=BD+CD=2\sqrt{2}+1$
∴CD=AD=1
$AB=\frac {AD}{sinB}=3,$$BD=\sqrt{AB²-AD²}= 2\sqrt{2},$
∴$BC=BD+CD=2\sqrt{2}+1$
1. 如图,在矩形$ABCD$中,对角线$AC$、$BD$相交于点$O$,$\angle BOC = 120^{\circ}$,$AB = 2$.
(1) 求$AC$、$BD$的长.
(2) 过点$O$作$OE \perp AD$,垂足为$E$,连接$BE$.设$\angle ABE = \alpha$,求$\tan \alpha$的值.

(1) 求$AC$、$BD$的长.
(2) 过点$O$作$OE \perp AD$,垂足为$E$,连接$BE$.设$\angle ABE = \alpha$,求$\tan \alpha$的值.

答案:解: (1)∵∠BOC=120°
∴∠AOB=60°
∴△AOB为等边三 角形
∴AO=AB=2
∴AC=2AO=4
∴BD=AC=4,$BC=\sqrt{AC²-AB²}= 2\sqrt{3}$
(2)∵OE⊥AD
∴$OE=\frac {1}{2}AB= 1$
$AE=\sqrt{AO²-OE²}=\sqrt{3}$
∴$tan α =\frac {AE}{AB}=\frac {\sqrt{3}}{2}$
∴∠AOB=60°
∴△AOB为等边三 角形
∴AO=AB=2
∴AC=2AO=4
∴BD=AC=4,$BC=\sqrt{AC²-AB²}= 2\sqrt{3}$
(2)∵OE⊥AD
∴$OE=\frac {1}{2}AB= 1$
$AE=\sqrt{AO²-OE²}=\sqrt{3}$
∴$tan α =\frac {AE}{AB}=\frac {\sqrt{3}}{2}$
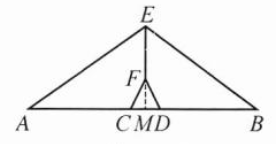
2. 如图是一座独塔双索结构的斜拉桥,某学习小组利用课余时间测量主塔顶端到桥面的距离,勘测记录如下表:

请利用表中提供的信息,求主塔顶端$E$到$AB$的距离(参考数据:$\sin 28^{\circ} \approx 0.47$,$\cos 28^{\circ} \approx 0.88$,$\tan 28^{\circ} \approx 0.53$).


请利用表中提供的信息,求主塔顶端$E$到$AB$的距离(参考数据:$\sin 28^{\circ} \approx 0.47$,$\cos 28^{\circ} \approx 0.88$,$\tan 28^{\circ} \approx 0.53$).

答案:
解:主塔顶端E到AB的距离约为$ 47.7\ \mathrm {m}$
延长EF{交}AB于点M
∵ EF⊥AB,点A、C分别与点B、D关于直线EF对称,$CD=12\ \mathrm {m} $
∴ ∠AME=90°,$CM=DM=\frac {1}{2}\ \mathrm {CD}=6(\mathrm {m})$
∵ ∠A=28°,$AC=84\ \mathrm {m}$
∴$AM=AC+CM=90(\mathrm {m})$
∴$tan A=\frac {EM}{AM}≈0.53$
∴$ EM≈47.7(\mathrm {m})$
解:主塔顶端E到AB的距离约为$ 47.7\ \mathrm {m}$
延长EF{交}AB于点M
∵ EF⊥AB,点A、C分别与点B、D关于直线EF对称,$CD=12\ \mathrm {m} $
∴ ∠AME=90°,$CM=DM=\frac {1}{2}\ \mathrm {CD}=6(\mathrm {m})$
∵ ∠A=28°,$AC=84\ \mathrm {m}$
∴$AM=AC+CM=90(\mathrm {m})$
∴$tan A=\frac {EM}{AM}≈0.53$
∴$ EM≈47.7(\mathrm {m})$
