4. 某地种植水稻获得突破性进展,小华和小莹到水稻种植基地调研。小莹根据水稻年产量数据,分别在直角坐标系中描出表示 2019—2023 年①号田和②号田年产量情况的点(记 2019 年为第 1 年度,横轴表示年度,纵轴表示年产量),如下图。
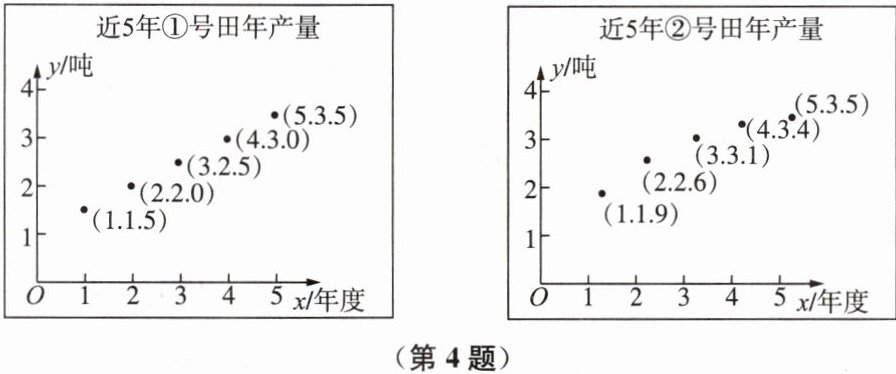
小华认为,可以从 $ y = kx + b(k>0) $,$ y=\frac{m}{x}(m>0) $,$ y=-0.1x^{2}+ax + c $ 中选择适当的函数模型,模拟①号田和②号田的年产量变化趋势。
(1) 请从小华提供的函数模型中,选择适当的模型分别模拟①号田和②号田的年产量变化趋势,并求出函数表达式;
(2) 请根据(1)中你选择的函数模型,预测①号田和②号田总年产量在哪一年最大,最大是多少?

小华认为,可以从 $ y = kx + b(k>0) $,$ y=\frac{m}{x}(m>0) $,$ y=-0.1x^{2}+ax + c $ 中选择适当的函数模型,模拟①号田和②号田的年产量变化趋势。
(1) 请从小华提供的函数模型中,选择适当的模型分别模拟①号田和②号田的年产量变化趋势,并求出函数表达式;
(2) 请根据(1)中你选择的函数模型,预测①号田和②号田总年产量在哪一年最大,最大是多少?
答案: 解:(1)(2)①号田符合函数模型y=kx+b(k>0),
将(1,1.5),(2,2.0)代入,得$\begin {cases}{k+b=1.5}\\{2k+b=2}\end {cases},$
解得$\begin {cases}{k=0.5}\\{b=1.}\end {cases}$
∴①号田的函数表达式为y=0.5x+1;
检验,当x=4时,y=2+1=3,符合题意.
②号田符合函数模型y=-0.1x²+ax+c,
将(1,1.9),(2,2.6)代入,得$\begin {cases}{-0.1+a+c=1.9}\\{-0.4+2a+c=2.6}\end {cases},$
解得$\begin {cases}{a=1}\\{c=1.}\end {cases}$
∴②号田的函数表达式为y=-0.1x²+x+1.
检验,当x=4时,y=-1.6+4+1=3.4,符合题意.
(3)设总年产量为w,依题意得w=-0.1x²+x+1+0.5x+1
=-0.1x²+ 1.5x+2=-0.1(x-7.5)²+7.625.
∵-0.1<0,
∴当x=7.5时,函数有最大值,
∴在2023年和2024年总年产量最大,最大是7.6吨.
将(1,1.5),(2,2.0)代入,得$\begin {cases}{k+b=1.5}\\{2k+b=2}\end {cases},$
解得$\begin {cases}{k=0.5}\\{b=1.}\end {cases}$
∴①号田的函数表达式为y=0.5x+1;
检验,当x=4时,y=2+1=3,符合题意.
②号田符合函数模型y=-0.1x²+ax+c,
将(1,1.9),(2,2.6)代入,得$\begin {cases}{-0.1+a+c=1.9}\\{-0.4+2a+c=2.6}\end {cases},$
解得$\begin {cases}{a=1}\\{c=1.}\end {cases}$
∴②号田的函数表达式为y=-0.1x²+x+1.
检验,当x=4时,y=-1.6+4+1=3.4,符合题意.
(3)设总年产量为w,依题意得w=-0.1x²+x+1+0.5x+1
=-0.1x²+ 1.5x+2=-0.1(x-7.5)²+7.625.
∵-0.1<0,
∴当x=7.5时,函数有最大值,
∴在2023年和2024年总年产量最大,最大是7.6吨.
例 在 5 张相同的小纸条上,分别写有$-1$、$0$、$1$、正数、负数.将这 5 张小纸条做成 5 支签,$-1$、$0$、$1$放在不透明的盒子$A$中搅匀,正数、负数放在不透明的盒子$B$中搅匀.
(1)从盒子$A$中任意抽出 1 支签,抽到$0$的概率是
(2)先从盒子$A$中任意抽出 1 支签,再从盒子$B$中任意抽出 1 支签.请用画树状图的方法,求抽到的数与文字描述相符合的概率.
(1)从盒子$A$中任意抽出 1 支签,抽到$0$的概率是
$\frac{1}{3}$
.(2)先从盒子$A$中任意抽出 1 支签,再从盒子$B$中任意抽出 1 支签.请用画树状图的方法,求抽到的数与文字描述相符合的概率.
答案:例 (1)$\frac{1}{3}$;(2)$\frac{1}{3}$.
解析:
(1)$\frac{1}{3}$
(2)树状图如下:
```
开始
|
+------+------+
| | |
-1 0 1
| | |
+---+ +---+ +---+
|正数| |正数| |正数|
|负数| |负数| |负数|
```
共有6种等可能的结果,其中符合的有2种(-1与负数,1与正数),概率为$\frac{2}{6}=\frac{1}{3}$
(2)树状图如下:
```
开始
|
+------+------+
| | |
-1 0 1
| | |
+---+ +---+ +---+
|正数| |正数| |正数|
|负数| |负数| |负数|
```
共有6种等可能的结果,其中符合的有2种(-1与负数,1与正数),概率为$\frac{2}{6}=\frac{1}{3}$