4. 如图,在一个天平左、右两端托盘上,分别放置质量为 20 g 和 70 g 的物品.现从质量为 10 g、20 g、30 g、40 g 的四件物品中,随机选取两件放在天平左端的托盘上,求天平平衡的概率.


答案:4.$\frac{1}{3}$.
解析:
从10g、20g、30g、40g的四件物品中随机选取两件,所有可能的结果有:(10,20)、(10,30)、(10,40)、(20,30)、(20,40)、(30,40),共6种。
天平左端初始质量为20g,设选取的两件物品质量分别为$m_1$、$m_2$,要使天平平衡,则左端总质量等于右端质量70g,即$20 + m_1 + m_2 = 70$,解得$m_1 + m_2 = 50$。
满足$m_1 + m_2 = 50$的情况有:(10,40)、(20,30),共2种。
所以天平平衡的概率为$\frac{2}{6} = \frac{1}{3}$。
$\frac{1}{3}$
天平左端初始质量为20g,设选取的两件物品质量分别为$m_1$、$m_2$,要使天平平衡,则左端总质量等于右端质量70g,即$20 + m_1 + m_2 = 70$,解得$m_1 + m_2 = 50$。
满足$m_1 + m_2 = 50$的情况有:(10,40)、(20,30),共2种。
所以天平平衡的概率为$\frac{2}{6} = \frac{1}{3}$。
$\frac{1}{3}$
5. 生活在数字时代的我们,很多场合会用二维码来表示不同的信息. 类似地,可通过在矩形网格中,对每一个小方格涂色或不涂色所得的图形来表示不同的信息.例如,只有一个小方格(图①)时,通过涂色或不涂色可表示两个不同的信息.

(1)用画树状图的方法,求图②可表示不同信息的总个数;(图中数字 1、2 表示两个不同位置的小方格,下同)
(2)图③为$2× 2$的网格图,它可表示不同信息的总个数为
(3)某校需要给每位师生制作一张“校园出入证”,准备用上述涂色方法在证件右下角采用$n× n$的网格图来表示各人身份信息,若该校师生共 492 人,则$n$的最小值为

(1)用画树状图的方法,求图②可表示不同信息的总个数;(图中数字 1、2 表示两个不同位置的小方格,下同)
(2)图③为$2× 2$的网格图,它可表示不同信息的总个数为
16个
;(3)某校需要给每位师生制作一张“校园出入证”,准备用上述涂色方法在证件右下角采用$n× n$的网格图来表示各人身份信息,若该校师生共 492 人,则$n$的最小值为
3
.答案:
16个
3
解: (1)树状图如下:
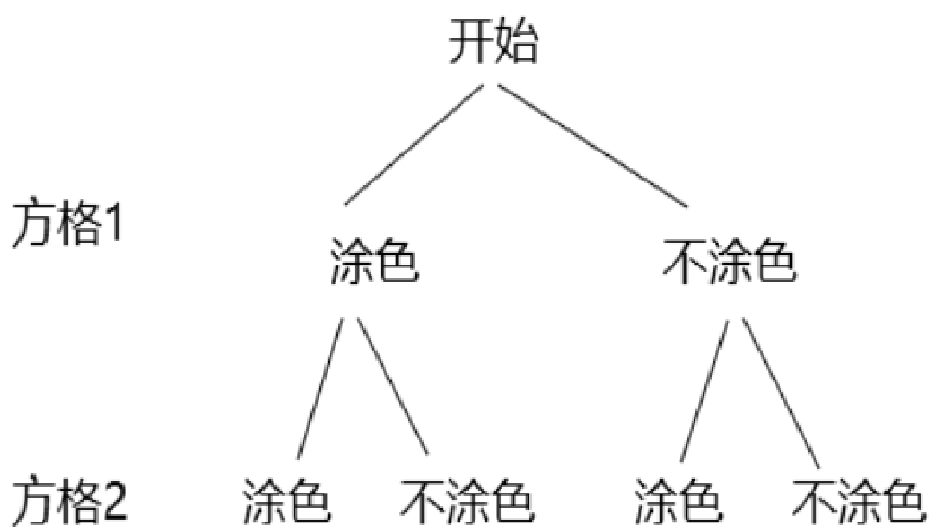
共有4种等可能的结果,
所以图②可表示不同信息的总个数为4个。
16个
3
解: (1)树状图如下:

共有4种等可能的结果,
所以图②可表示不同信息的总个数为4个。