3. 在一个不透明的盒子里装有黑、白两种颜色的球共 40 个,这些球除颜色外其余完全相同.小颖从盒子里随机摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程,结果如下:

(1)当摸球的次数很大时,摸到白球的概率将会接近
(2)在下列实验中,哪些事件的概率符合(1)中的估算结果?请写出序号,并说明理由.
① 投掷一枚均匀的硬币,落到桌面上恰好是正面朝上.
② 掷一个质地均匀的正方体骰子(面的点数分别为 1 到 6),落地时面朝上点数“大于 4”.
③ 从一副不含大小王的扑克牌中任意抽取一张,这张牌是“红桃”.
④ 在一道单选题 $ A $、$ B $、$ C $、$ D $ 四个选项任选一个,正好选中正确选项.

(1)当摸球的次数很大时,摸到白球的概率将会接近
0.25
(精确到 0.01).(2)在下列实验中,哪些事件的概率符合(1)中的估算结果?请写出序号,并说明理由.
① 投掷一枚均匀的硬币,落到桌面上恰好是正面朝上.
② 掷一个质地均匀的正方体骰子(面的点数分别为 1 到 6),落地时面朝上点数“大于 4”.
③ 从一副不含大小王的扑克牌中任意抽取一张,这张牌是“红桃”.
④ 在一道单选题 $ A $、$ B $、$ C $、$ D $ 四个选项任选一个,正好选中正确选项.
答案:3.(1)0.25;(2)③④.
解析:
3.(1)0.25;
(2)③④。理由如下:
①投掷一枚均匀的硬币,正面朝上的概率为$\frac{1}{2}=0.5$,不符合;
②掷质地均匀的正方体骰子,点数“大于4”的概率为$\frac{2}{6}=\frac{1}{3}\approx0.33$,不符合;
③从不含大小王的扑克牌中抽一张是“红桃”的概率为$\frac{13}{52}=0.25$,符合;
④单选题四选一选中正确选项的概率为$\frac{1}{4}=0.25$,符合。
(2)③④。理由如下:
①投掷一枚均匀的硬币,正面朝上的概率为$\frac{1}{2}=0.5$,不符合;
②掷质地均匀的正方体骰子,点数“大于4”的概率为$\frac{2}{6}=\frac{1}{3}\approx0.33$,不符合;
③从不含大小王的扑克牌中抽一张是“红桃”的概率为$\frac{13}{52}=0.25$,符合;
④单选题四选一选中正确选项的概率为$\frac{1}{4}=0.25$,符合。
4. 在对某校体育活动的调查中,形成了如下调查报告(不完整):
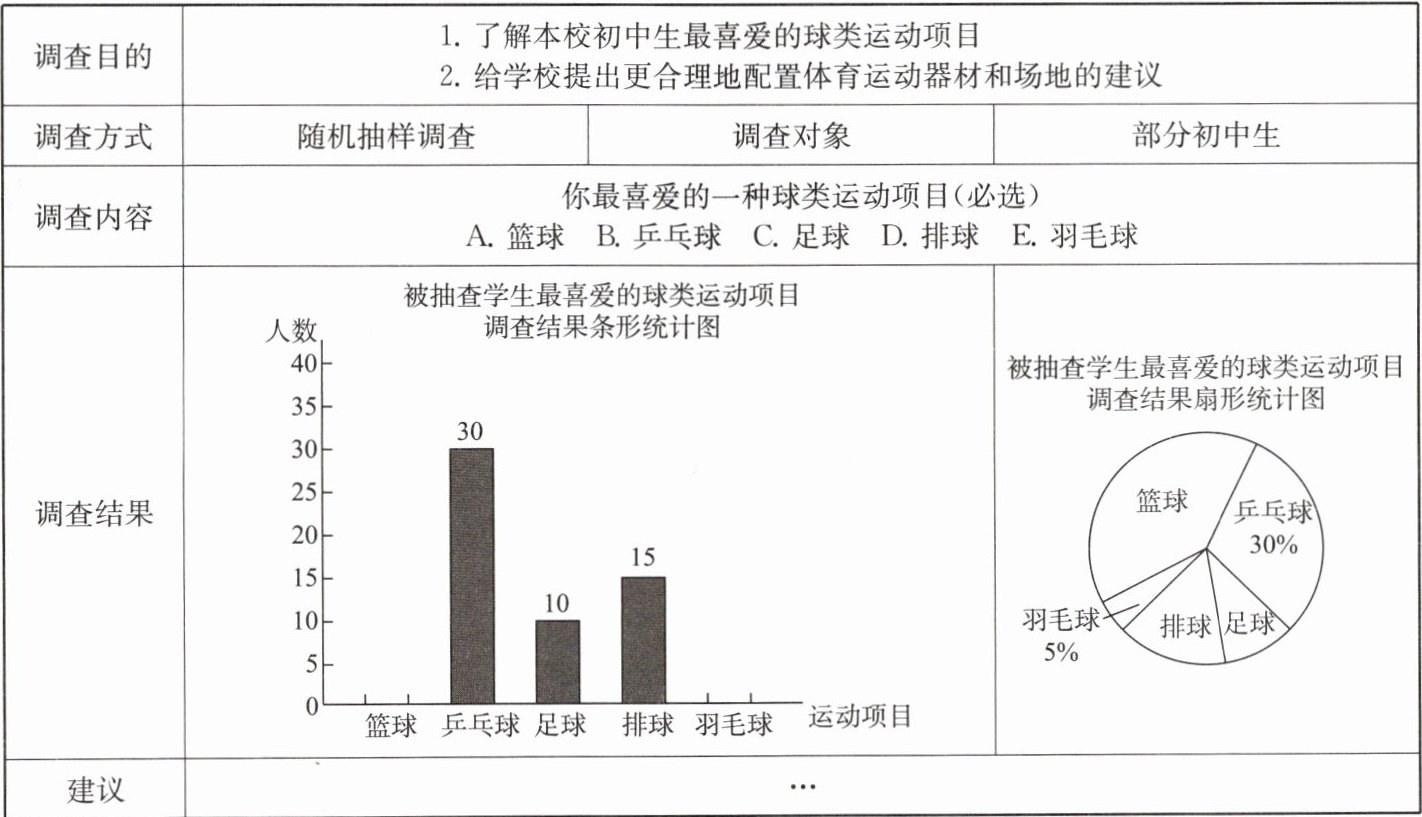
结合调查信息,回答下列问题:
(1)本次调查共抽查了多少名学生?
(2)估计该校 900 名初中生中最喜爱篮球项目的人数.
(3)请根据调查结果向该校提一条合理的建议.

结合调查信息,回答下列问题:
(1)本次调查共抽查了多少名学生?
(2)估计该校 900 名初中生中最喜爱篮球项目的人数.
(3)请根据调查结果向该校提一条合理的建议.
答案:解:(1)被抽查学生数: 30÷30\% = 100,
答:本次调查共抽查了100名学生.
(2)被抽查的100人中最喜爱羽毛球的人数为: 100×5\% =5,
.被抽查的100人中最喜爱篮球的人数为:
100- 30- 10-15-5= 40,
$900×\frac {40}{100}=360 ($人).
答:估计该校900名初中生中最喜爱篮球项目的人数为360.
(3)因为喜欢篮球的学生较多,建议学校多配置篮球器材、增加篮球场地等.
答:本次调查共抽查了100名学生.
(2)被抽查的100人中最喜爱羽毛球的人数为: 100×5\% =5,
.被抽查的100人中最喜爱篮球的人数为:
100- 30- 10-15-5= 40,
$900×\frac {40}{100}=360 ($人).
答:估计该校900名初中生中最喜爱篮球项目的人数为360.
(3)因为喜欢篮球的学生较多,建议学校多配置篮球器材、增加篮球场地等.