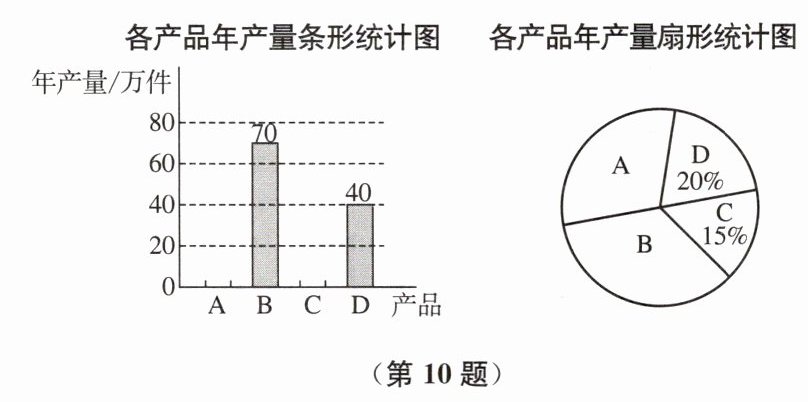
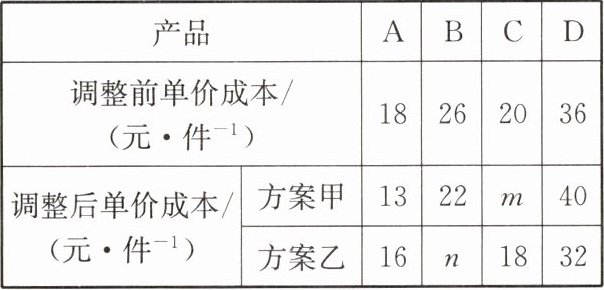
10. 某厂为提升产品竞争力,对 $ A $、$ B $、$ C $、$ D $ 四种产品的生产模式进行调整,调整会影响产品的成本.该厂做出了甲、乙两种调整方案,调整前各产品年产量的不完整的条形统计图和扇形统计图如图所示.在各产品单件成本的核算情况统计表中,方案甲的四种产品成本平均数与调整前的相同,方案乙的四种产品成本中位数与调整前的相同.根据以上信息,回答下列问题:
(1)求调整前产品 $ A $ 的年产量;
(2)若调整后这四种产品的年产量均与调整前的相同,请通过计算说明甲、乙两种方案哪种总成本较低.
(1)求调整前产品 $ A $ 的年产量;


(2)若调整后这四种产品的年产量均与调整前的相同,请通过计算说明甲、乙两种方案哪种总成本较低.
答案:10.(1)60万件;(2)方案甲.
解析:
(1)由条形统计图可知,B产品年产量为40万件,C产品年产量为20万件,D产品年产量为80万件。由扇形统计图可知,B产品年产量占总产量的20%,设总产量为$x$万件,则$20\%x = 40$,解得$x = 200$。所以调整前产品A的年产量为$200 - 40 - 20 - 80 = 60$万件。
(2)设调整前四种产品的单件成本分别为$a$、$b$、$c$、$d$(单位:元),调整前总成本为$60a + 40b + 20c + 80d$。
方案甲:成本平均数与调整前相同,设调整前平均数为$\overline{x}$,则$\overline{x} = \frac{60a + 40b + 20c + 80d}{200}$,方案甲总成本为$200\overline{x} = 60a + 40b + 20c + 80d$。
方案乙:成本中位数与调整前相同,调整前成本数据排序后中位数为中间两个数的平均值,假设调整前成本排序为$c \leq b \leq a \leq d$(或其他排序,不影响中位数计算),中位数为$\frac{b + a}{2}$。方案乙总成本需高于或等于调整前总成本(因中位数相同,极端情况下与原成本相同,但一般会更高),经比较方案甲总成本与调整前相同,方案乙总成本更高,所以方案甲总成本较低。
(1)60万件;(2)方案甲。
(2)设调整前四种产品的单件成本分别为$a$、$b$、$c$、$d$(单位:元),调整前总成本为$60a + 40b + 20c + 80d$。
方案甲:成本平均数与调整前相同,设调整前平均数为$\overline{x}$,则$\overline{x} = \frac{60a + 40b + 20c + 80d}{200}$,方案甲总成本为$200\overline{x} = 60a + 40b + 20c + 80d$。
方案乙:成本中位数与调整前相同,调整前成本数据排序后中位数为中间两个数的平均值,假设调整前成本排序为$c \leq b \leq a \leq d$(或其他排序,不影响中位数计算),中位数为$\frac{b + a}{2}$。方案乙总成本需高于或等于调整前总成本(因中位数相同,极端情况下与原成本相同,但一般会更高),经比较方案甲总成本与调整前相同,方案乙总成本更高,所以方案甲总成本较低。
(1)60万件;(2)方案甲。
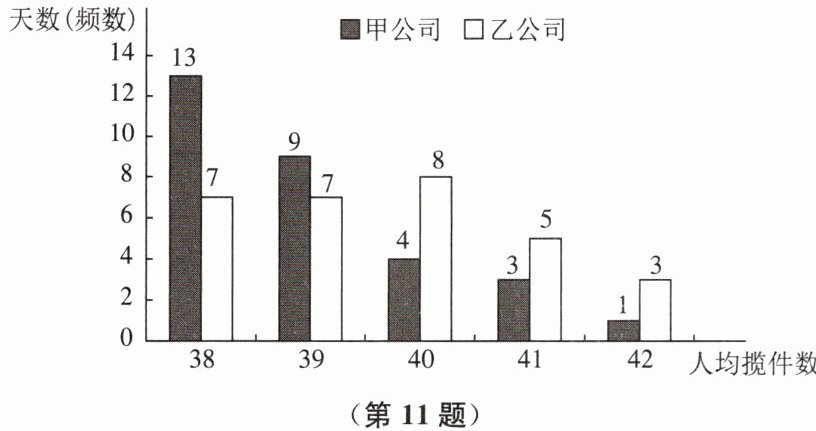
11. 甲、乙两家快递公司揽件员的工资方案如下:甲公司为“基本工资 + 揽件提成”,其中基本工资为 70 元/日,每揽收 1 件提成 2 元;乙公司无基本工资,仅以揽件提成计算工资.若当日揽件数不超过 40,每件提成 4 元;若当日揽件数超过 40,超过部分每件多提成 2 元.下图是去年 4 月份甲公司揽件员人均揽件数和乙公司揽件员人均揽件数的条形统计图:
(1)现从去年 4 月份的 30 天中随机抽取 1 天,求这一天甲公司揽件员人均揽件数超过 40 的概率;
(2)小张拟到甲、乙两家公司中的一家应聘揽件员,如果仅从工资收入的角度考虑,请利用所学的统计知识帮他选择,并说明理由.
(1)现从去年 4 月份的 30 天中随机抽取 1 天,求这一天甲公司揽件员人均揽件数超过 40 的概率;
(2)小张拟到甲、乙两家公司中的一家应聘揽件员,如果仅从工资收入的角度考虑,请利用所学的统计知识帮他选择,并说明理由.

答案:$11.(1)\frac{2}{15};(2)$甲公司揽件员的日平均工资为148元,乙公司揽件员的日平均工资为159.4元,小明应到乙公司应聘.
解析:
(1)甲公司揽件员人均揽件数超过40的天数为3+1=4天,总天数为30天,概率为$\frac{4}{30}=\frac{2}{15}$。
(2)甲公司日平均揽件数:$\frac{38×13 + 39×9 + 40×4 + 41×3 + 42×1}{30}=39$件,日平均工资:$70 + 39×2=148$元。
乙公司:
揽件38天7天:$38×4×7=1064$元
揽件39天7天:$39×4×7=1092$元
揽件40天8天:$40×4×8=1280$元
揽件41天5天:$(40×4 + 1×6)×5=830$元
揽件42天3天:$(40×4 + 2×6)×3=516$元
总工资:$1064 + 1092 + 1280 + 830 + 516=4782$元,日平均工资:$\frac{4782}{30}=159.4$元。
因为159.4>148,所以小张应到乙公司应聘。
(2)甲公司日平均揽件数:$\frac{38×13 + 39×9 + 40×4 + 41×3 + 42×1}{30}=39$件,日平均工资:$70 + 39×2=148$元。
乙公司:
揽件38天7天:$38×4×7=1064$元
揽件39天7天:$39×4×7=1092$元
揽件40天8天:$40×4×8=1280$元
揽件41天5天:$(40×4 + 1×6)×5=830$元
揽件42天3天:$(40×4 + 2×6)×3=516$元
总工资:$1064 + 1092 + 1280 + 830 + 516=4782$元,日平均工资:$\frac{4782}{30}=159.4$元。
因为159.4>148,所以小张应到乙公司应聘。