12. 某商场“五一”期间举办了抽奖促销活动.活动规定:凡在商场消费一定金额的顾客,均可获得一次抽奖机会.抽奖方案如下:从装有大小质地完全相同的 1 个红球和编号为①、②、③的 3 个黄球的袋中,随机摸出 1 个球.若摸得红球,则中奖,可获得奖品;若摸得黄球,则不中奖.同时,还允许未中奖的顾客将摸得的球放回袋中,然后往袋中加入 1 个红球或黄球后,再从袋中摸出 1 个球,记下颜色后不放回,最后再从袋中摸出 1 个球,若摸得的两球颜色相同,则该顾客可获得礼品一份.现已知某顾客获得抽奖机会.
(1)求该顾客首次摸球中奖的概率.
(2)假如该顾客首次摸球未中奖,为了有更大机会获得礼品,他应往袋中加入哪种颜色的球?说明你的理由.
(1)求该顾客首次摸球中奖的概率.
(2)假如该顾客首次摸球未中奖,为了有更大机会获得礼品,他应往袋中加入哪种颜色的球?说明你的理由.
答案:
解:(1)顾客首次摸球的所有可能结果为红,黄①,黄②,黄③,
共4种等可能的结果,
记“首次摸得红球”为事件A,则事件A发生的结果只有1种,
∴$P(\mathrm {A})=\frac {1}{4},$
∴顾客首次摸球中奖的概率为$ \frac {1}{4}.$
(2)他应往袋中加入黄球;理由如下:
记往袋中加入的球为“新”,摸得的两球所有可能的结果列表如下:
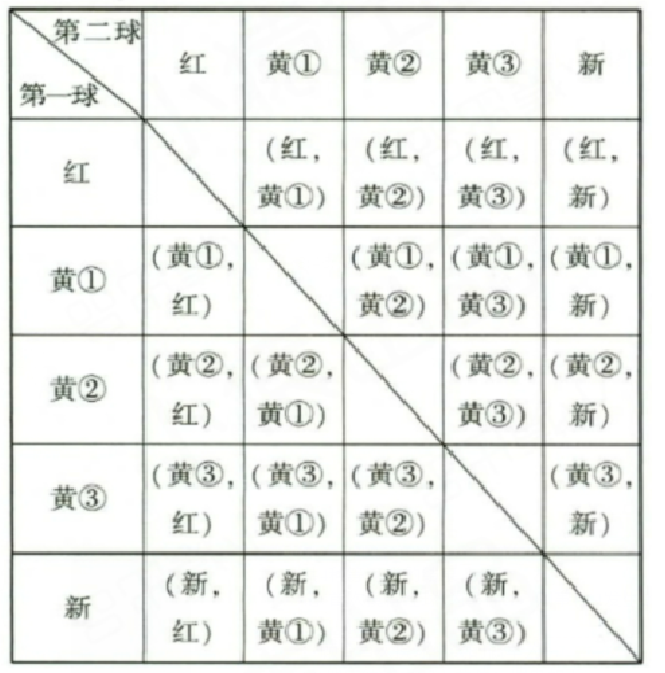
共有20种等可能结果,$(\mathrm {i})$若往袋中加入的是红球,两球颜色相同的结果共有8种,
此时该顾客获得精美礼品的概率$ P_1=\frac {8}{20}=\frac {2}{5};$
$(\mathrm {ii})$若往袋中加入的是黄球,两球颜色相同的结果共有12种,
此时该顾客获得精美礼品的概率$ P_2=\frac {12}{20}=\frac {3}{5};$
∵$\frac {2}{5}<\frac {3}{5},$
∴$P_1<P_2,$
∴他应往袋中加入黄球.
解: (1)P(甲公司揽件员人均揽件数超过$40)=\frac {3+1}{30}=\frac {2}{15}$
(2)甲公司平均月工资: 70×30+2×(38×13+39×9+40×4
+41×3+42×1)=4440(元)
乙公司平均月工资: 4×(38×7+39×7+40×8+41×5+42×3)
+2×(1×5+2×3)=4782(元)
4782元> 4440元
所以选择乙公司
解:(1)顾客首次摸球的所有可能结果为红,黄①,黄②,黄③,
共4种等可能的结果,
记“首次摸得红球”为事件A,则事件A发生的结果只有1种,
∴$P(\mathrm {A})=\frac {1}{4},$
∴顾客首次摸球中奖的概率为$ \frac {1}{4}.$
(2)他应往袋中加入黄球;理由如下:
记往袋中加入的球为“新”,摸得的两球所有可能的结果列表如下:

共有20种等可能结果,$(\mathrm {i})$若往袋中加入的是红球,两球颜色相同的结果共有8种,
此时该顾客获得精美礼品的概率$ P_1=\frac {8}{20}=\frac {2}{5};$
$(\mathrm {ii})$若往袋中加入的是黄球,两球颜色相同的结果共有12种,
此时该顾客获得精美礼品的概率$ P_2=\frac {12}{20}=\frac {3}{5};$
∵$\frac {2}{5}<\frac {3}{5},$
∴$P_1<P_2,$
∴他应往袋中加入黄球.
解: (1)P(甲公司揽件员人均揽件数超过$40)=\frac {3+1}{30}=\frac {2}{15}$
(2)甲公司平均月工资: 70×30+2×(38×13+39×9+40×4
+41×3+42×1)=4440(元)
乙公司平均月工资: 4×(38×7+39×7+40×8+41×5+42×3)
+2×(1×5+2×3)=4782(元)
4782元> 4440元
所以选择乙公司