15. (8分)某化工材料经销公司购进了一种化工原料共 $ 7000 \mathrm{ kg} $,购进价格为 $ 30 \mathrm{ 元/kg} $。物价部门规定其销售单价不得高于每千克70元,也不得低于30元。市场调查发现:单价定为70元时,日均销售 $ 60 \mathrm{ kg} $;单价每降低1元,日均多售出 $ 2 \mathrm{ kg} $。在销售过程中,每天还要支出其他费用500元(天数不足一天时,按整天计算)。设销售单价为 $ x $ 元,日均获利为 $ y $ 元。
(1)求 $ y $ 与 $ x $ 之间的函数表达式,并注明 $ x $ 的取值范围。
(2)当单价定为多少元时日均获利最多?最多是多少元?
(1)求 $ y $ 与 $ x $ 之间的函数表达式,并注明 $ x $ 的取值范围。
(2)当单价定为多少元时日均获利最多?最多是多少元?
答案:解:(1)由题意得,
y=(x- 30)[60 + 2(70 -x)]-500
= (x- 30)(200-2x)-500
=-2x²+ 260x-6500
函数表达式为y=-2x²+260x-6500,30≤x≤70
(2)y= -2x²+260x-6500
=-2(x-65)²+1950
所以当x = 65时, y取最大值,最大值为1950 ,
即当单价定为65元时日均获利最多,最多是1950元。
y=(x- 30)[60 + 2(70 -x)]-500
= (x- 30)(200-2x)-500
=-2x²+ 260x-6500
函数表达式为y=-2x²+260x-6500,30≤x≤70
(2)y= -2x²+260x-6500
=-2(x-65)²+1950
所以当x = 65时, y取最大值,最大值为1950 ,
即当单价定为65元时日均获利最多,最多是1950元。
16. (8分)如图,在矩形 $ ABCD $ 中,$ AB = 3 $,$ BC = 6 $,动点 $ E $ 从点 $ A $ 出发,以每秒1个单位长度的速度向点 $ B $ 运动;动点 $ F $ 从点 $ B $ 出发,以每秒2个单位长度的速度向点 $ C $ 运动。求 $ \triangle DEF $ 的面积 $ S $ 与运动时间 $ t $ 之间的函数表达式,并指出当 $ t $ 取何值时,$ \triangle DEF $ 的面积 $ S $ 取得最小值。
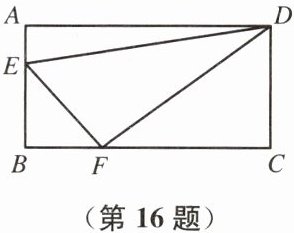

答案:解:由题意得, AD=BC=6 , AB=CD=3 , AE=t, BE=3-t ,
BF=2t, CF=6-2t
$S= S_{矩形ABCD}-S_{△ADE}-S_{△BEF}-S_{△DFC}$
$=3×6-\frac {1}{2}×t×6-\frac {1}{2}×(3-t)×2t-\frac {1}{2}×(6-2t)×3$
= t²-3t+9
所以△DEF的面积S与运动时间之间的函数表达式为
S= t²- 3t+9
因为$S= t²-3t+9=(t-\frac {3}{2})²+\frac {27}{4}$
所以当$t=\frac {3}{2}$时,△DEF的面积S取得最小值。
BF=2t, CF=6-2t
$S= S_{矩形ABCD}-S_{△ADE}-S_{△BEF}-S_{△DFC}$
$=3×6-\frac {1}{2}×t×6-\frac {1}{2}×(3-t)×2t-\frac {1}{2}×(6-2t)×3$
= t²-3t+9
所以△DEF的面积S与运动时间之间的函数表达式为
S= t²- 3t+9
因为$S= t²-3t+9=(t-\frac {3}{2})²+\frac {27}{4}$
所以当$t=\frac {3}{2}$时,△DEF的面积S取得最小值。