4. 结合二次函数 $ y = x ^ { 2 } - 3 x - 4 $ 的图像可知:若 $ m ^ { 2 } - 3 m - 4 < 0 $,则 $ m $ 的取值范围为
-1< m< 4
.答案:(-1,0)和$(\frac {5}{3},$0)
-1<x<4
-1<x<4
三、解答题
5. 已知二次函数 $ y = x ^ { 2 } - 4 x - 5 $,画出这个二次函数的图像,根据图像回答下列问题:
(1) 方程 $ x ^ { 2 } - 4 x - 5 = 0 $ 的解是什么?
(2) 当 $ x $ 取何值时,函数值大于 $ 0 $?当 $ x $ 取何值时,函数值小于 $ 0 $?

5. 已知二次函数 $ y = x ^ { 2 } - 4 x - 5 $,画出这个二次函数的图像,根据图像回答下列问题:
(1) 方程 $ x ^ { 2 } - 4 x - 5 = 0 $ 的解是什么?
(2) 当 $ x $ 取何值时,函数值大于 $ 0 $?当 $ x $ 取何值时,函数值小于 $ 0 $?

答案:
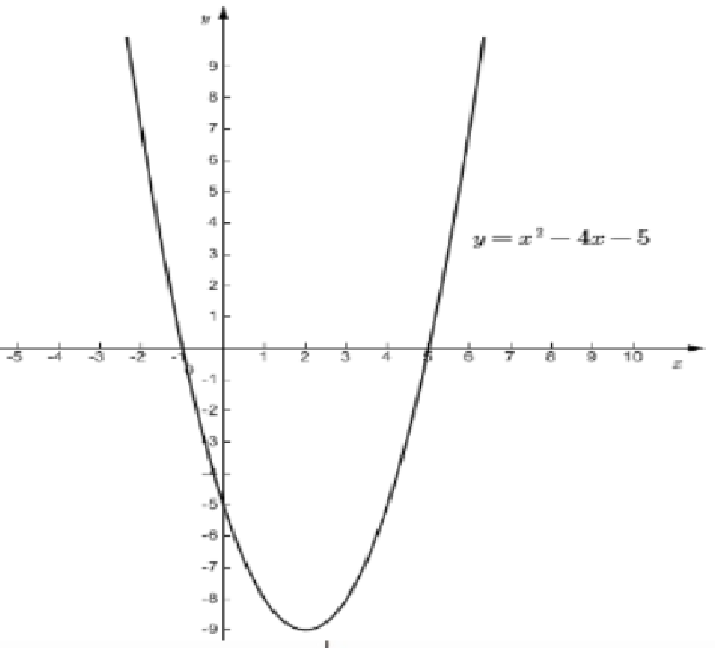
解:$(1)$方程$x²-4x-5=0$的解是
${x}_1=5,$${x}_2=-1.$
$(2)$根据函数图像可知$,$

当$x\lt - 1$或$x\gt 5$时,函数值大于$0;$
当$-1<x<5$时$,$函数值小于$0.$
6. 已知二次函数 $ y = x ^ { 2 } + b x - 1 $ 的图像经过点 $ ( 3, 2 ) $.
(1) 求这个二次函数的表达式;
(2) 画出它的图像,并写出图像的顶点坐标;
(3) 结合图像,请直接写出当 $ y \geq 2 $ 时 $ x $ 的取值范围.

(1) 求这个二次函数的表达式;
(2) 画出它的图像,并写出图像的顶点坐标;
(3) 结合图像,请直接写出当 $ y \geq 2 $ 时 $ x $ 的取值范围.

答案:解:(1)把(3, 2)代入y=x²+bx-1 ,
得9+ 3b- 1=2,得b=-2
所以y=x²- 2x- 1
(2)顶点坐标是(1,- 2)
(3)x≤-1或x≥3
得9+ 3b- 1=2,得b=-2
所以y=x²- 2x- 1
(2)顶点坐标是(1,- 2)
(3)x≤-1或x≥3