7. 若关于 $ x $ 的方程 $ x ^ { 2 } + p x + q = 0 $ 没有实数根,则函数 $ y = x ^ { 2 } - p x + q $ 的图像的顶点一定在(
A.$ x $ 轴的上方
B.$ x $ 轴的下方
C.$ x $ 轴上
D.$ y $ 轴上
A
)A.$ x $ 轴的上方
B.$ x $ 轴的下方
C.$ x $ 轴上
D.$ y $ 轴上
答案:A
8. 已知函数 $ y = - x ^ { 2 } + ( m - 1 ) x + m $($ m $ 为常数).
(1) 该函数的图像与 $ x $ 轴的公共点的个数是(
A. $ 0 $
B. $ 1 $
C. $ 2 $
D. $ 1 $ 或 $ 2 $
(2) 求证:不论 $ m $ 为何值,该函数的图像的顶点都在函数 $ y = ( x + 1 ) ^ { 2 } $ 的图像上.
(3) 当 $ - 2 \leq m \leq 3 $ 时,求该函数图像顶点的纵坐标的取值范围.
(1) 该函数的图像与 $ x $ 轴的公共点的个数是(
D
)A. $ 0 $
B. $ 1 $
C. $ 2 $
D. $ 1 $ 或 $ 2 $
(2) 求证:不论 $ m $ 为何值,该函数的图像的顶点都在函数 $ y = ( x + 1 ) ^ { 2 } $ 的图像上.
(3) 当 $ - 2 \leq m \leq 3 $ 时,求该函数图像顶点的纵坐标的取值范围.
答案:D
解: (2)顶点坐标为$(\frac {m-1}{2},$$\frac {(m+1)²}{4})$
把$x=\frac {m-1}{2}$代入y= (x+1)²,
得$y=\frac {(m+1)²}{4}$
不论m为何值,该函数的图像的顶点都在函数y= (x +1)²的图像上
(3)设顶点纵坐标为z ,
则$z=\frac {(m+1)²}{4} $
当m=-1时,z有最小值0
当m=- 2时,$z=\frac {1}{4}$
当m=3时, z= 4
所以当-2≤m≤3时,0≤z≤4
解: (2)顶点坐标为$(\frac {m-1}{2},$$\frac {(m+1)²}{4})$
把$x=\frac {m-1}{2}$代入y= (x+1)²,
得$y=\frac {(m+1)²}{4}$
不论m为何值,该函数的图像的顶点都在函数y= (x +1)²的图像上
(3)设顶点纵坐标为z ,
则$z=\frac {(m+1)²}{4} $
当m=-1时,z有最小值0
当m=- 2时,$z=\frac {1}{4}$
当m=3时, z= 4
所以当-2≤m≤3时,0≤z≤4
例 1 利用函数的图像,求下列方程的解:
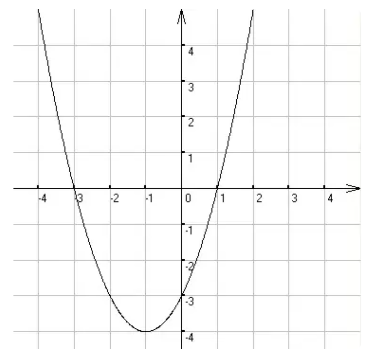
(1) $ x^{2}+2x - 3 = 0 $;
(2) $ 2x^{2}-5x + 2 = 0 $.
(1) $ x^{2}+2x - 3 = 0 $;
(2) $ 2x^{2}-5x + 2 = 0 $.
答案:
解:$(1){x}_1=-3,$${x}_2=1$
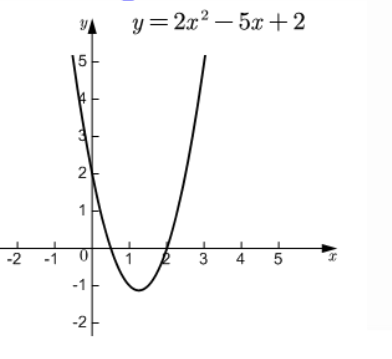
解:$(2){x}_1=\frac {1}{2},$${x}_2=2$
解:$(1){x}_1=-3,$${x}_2=1$

解:$(2){x}_1=\frac {1}{2},$${x}_2=2$

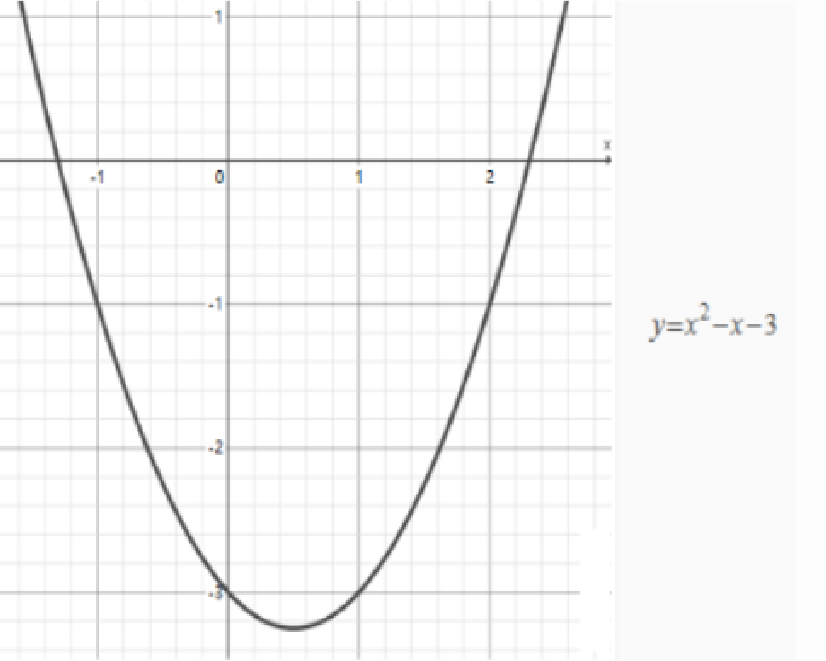
例 2 利用函数的图像,求方程 $ x^{2}-x - 3 = 0 $ 的近似解(精确到 0.1).
答案:
解:如图所示,方程的近似解为${x}_1≈-1.3 ,$${x}_2≈2.3$
解:如图所示,方程的近似解为${x}_1≈-1.3 ,$${x}_2≈2.3$
