例 2 已知 $ y = (k + 2)x^{k^{2} + k - 4} $ ( $ k $ 为常数),若 $ y $ 是 $ x $ 的二次函数,且当 $ x > 0 $ 时, $ y $ 随 $ x $ 的增大而增大.
(1) 求 $ k $ 的值;
(2) 求这个二次函数的图像的顶点坐标和对称轴.
(1) 求 $ k $ 的值;
(2) 求这个二次函数的图像的顶点坐标和对称轴.
答案:解:共同点:顶点都是坐标原点,
对称轴都是y 轴.
不同点:开口方向不同.
解:(1)由题意可得:k+2>0,且k²+k-4=2
解得k=2
(2)由(1)得:k=2即y=4x²
所以顶点坐标为(0,0)
对称轴为y轴
对称轴都是y 轴.
不同点:开口方向不同.
解:(1)由题意可得:k+2>0,且k²+k-4=2
解得k=2
(2)由(1)得:k=2即y=4x²
所以顶点坐标为(0,0)
对称轴为y轴
1. 已知函数 $ y = 2x^{2} $,对于一切 $ x $ 的值,总有(
A.$ y > 0 $
B.$ y \geq 0 $
C.$ y < 0 $
D.$ y \leq 0 $
B
)A.$ y > 0 $
B.$ y \geq 0 $
C.$ y < 0 $
D.$ y \leq 0 $
答案:B
2. 下列关于函数 $ y = \frac{1}{2}x^{2} $ 的说法中,正确的是(
A.$ y $ 随 $ x $ 的增大而增大
B.$ y $ 随 $ x $ 的增大而减小
C.当 $ x > 0 $ 时, $ y $ 随 $ x $ 的增大而增大
D.当 $ x > 0 $ 时, $ y $ 随 $ x $ 的增大而减小
C
)A.$ y $ 随 $ x $ 的增大而增大
B.$ y $ 随 $ x $ 的增大而减小
C.当 $ x > 0 $ 时, $ y $ 随 $ x $ 的增大而增大
D.当 $ x > 0 $ 时, $ y $ 随 $ x $ 的增大而减小
答案:C
3. 二次函数 $ y = \frac{1}{3}x^{2} $ 的图像开口
向上
,顶点坐标为(0,0)
,对称轴为y 轴
.答案:向上
(0,0)
y轴
(0,0)
y轴
4. 已知二次函数 $ y = ax^{2}(a \neq 0) $,根据图像的对称性可知,若点 $ (2, - 3) $ 在它的图像上,则点(
-2
,-3
)也一定在它的图像上.答案:-2
-3
-3
三、解答题
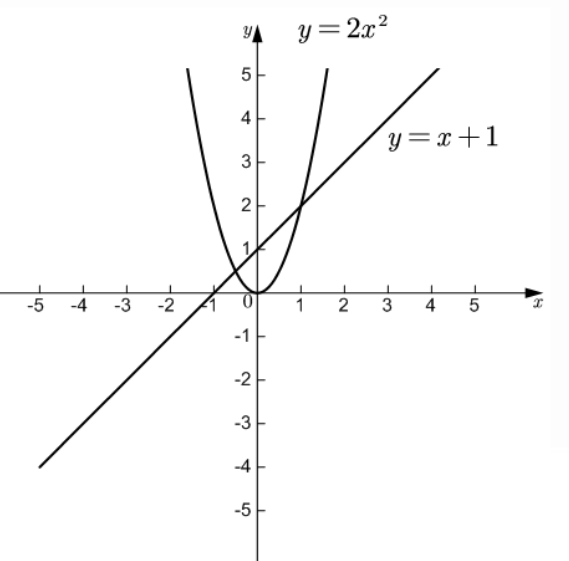
5. 请在同一平面直角坐标系中画出二次函数 $ y = 2x^{2} $ 与一次函数 $ y = x + 1 $ 的图像,并求出它们的交点坐标.
5. 请在同一平面直角坐标系中画出二次函数 $ y = 2x^{2} $ 与一次函数 $ y = x + 1 $ 的图像,并求出它们的交点坐标.
答案:
解:由题意可得:$\begin{cases}{y=2x² }\\{y=x+1} \end{cases}$
解得$\begin{cases}{x=1 }\\{y=2} \end{cases}$或$\begin{cases}{x=-\dfrac {1}{2} }\\{y=\dfrac {1}{2}} \end{cases}$
所以交点坐标为(1,2)或$(-\frac {1}{2},$$\frac {1}{2})$
解:由题意可得:$\begin{cases}{y=2x² }\\{y=x+1} \end{cases}$
解得$\begin{cases}{x=1 }\\{y=2} \end{cases}$或$\begin{cases}{x=-\dfrac {1}{2} }\\{y=\dfrac {1}{2}} \end{cases}$
所以交点坐标为(1,2)或$(-\frac {1}{2},$$\frac {1}{2})$
