6. 已知等边三角形的边长为 $ 2x $,请将此三角形的面积 $ S $ 表示成 $ x $ 的函数,并画出这个函数图像的草图.
答案:
解:$S=\frac {1}{2}×2x×\sqrt{3}x=\sqrt{3}x²,$其中$x\gt 0$
函数图像的草图如下:
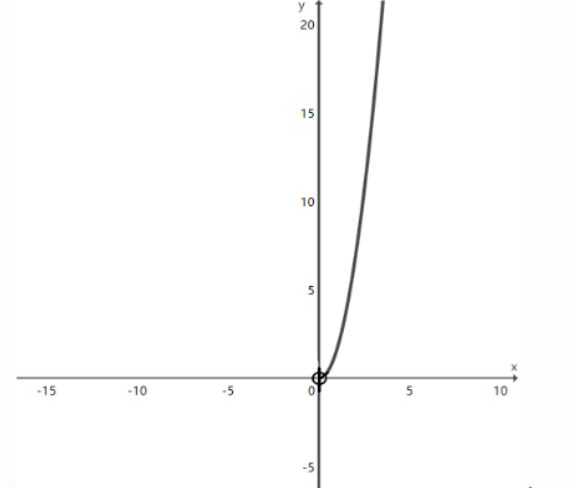
解:$S=\frac {1}{2}×2x×\sqrt{3}x=\sqrt{3}x²,$其中$x\gt 0$
函数图像的草图如下:

7. 已知二次函数 $ y = ax^{2}(a \neq 0) $ 的图像与一次函数 $ y = 2x - 3 $ 的图像有一个公共点的坐标为 $ (1, b) $.
(1) 求 $ a $ 与 $ b $ 的值;
(2) 求这个二次函数图像的顶点坐标和对称轴;
(3) 若函数 $ y = ax^{2} $ 的值随 $ x $ 的增大而增大,请写出自变量 $ x $ 的取值范围.
(1) 求 $ a $ 与 $ b $ 的值;
(2) 求这个二次函数图像的顶点坐标和对称轴;
(3) 若函数 $ y = ax^{2} $ 的值随 $ x $ 的增大而增大,请写出自变量 $ x $ 的取值范围.
答案:解:(1)因为点(1 , b)在函数y= 2x-3图像上
所以b=2-3=-1
因为点(1 , -1)在二次函数y = ax²的图像上
所以a=-1
(2)顶点坐标(0 , 0) ,对称轴为y轴
(3)当x< 0时,函数y = ax²的值随x的增大而增大
所以b=2-3=-1
因为点(1 , -1)在二次函数y = ax²的图像上
所以a=-1
(2)顶点坐标(0 , 0) ,对称轴为y轴
(3)当x< 0时,函数y = ax²的值随x的增大而增大
8. 已知二次函数 $ y = (m - 1)x^{m^{2} - m} $ ( $ m $ 为常数)的图像开口向下,则 $ m $ 的值为(
A.2
B.- 1
C.2 或 - 1
D.2 或 1
B
)A.2
B.- 1
C.2 或 - 1
D.2 或 1
答案:B