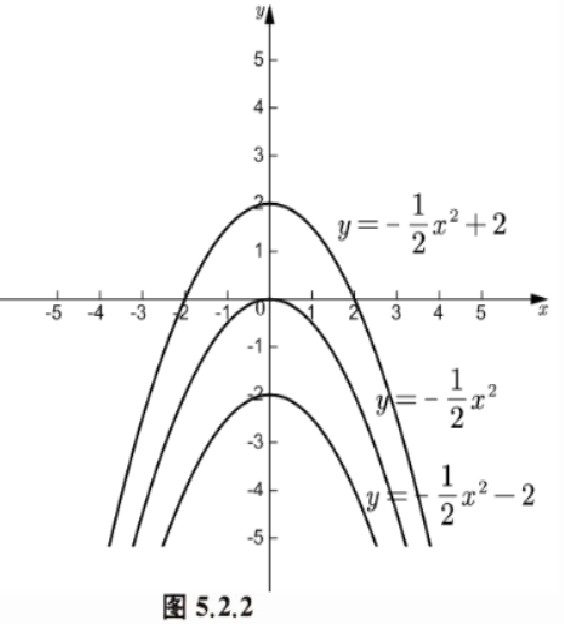
例 1 在如图 5.2.2 所示的平面直角坐标系中，分别画出下列二次函数的图像：
(1) $ y = -\frac{1}{2}x^{2} $；(2) $ y = -\frac{1}{2}x^{2} + 2 $；(3) $ y = -\frac{1}{2}x^{2} - 2 $。
观察三个图像的相互关系，并分别指出它们的开口方向及对称轴、顶点的位置。你能说出二次函数 $ y = -\frac{1}{2}x^{2} + k $ 的图像的开口方向及对称轴、顶点的位置吗？

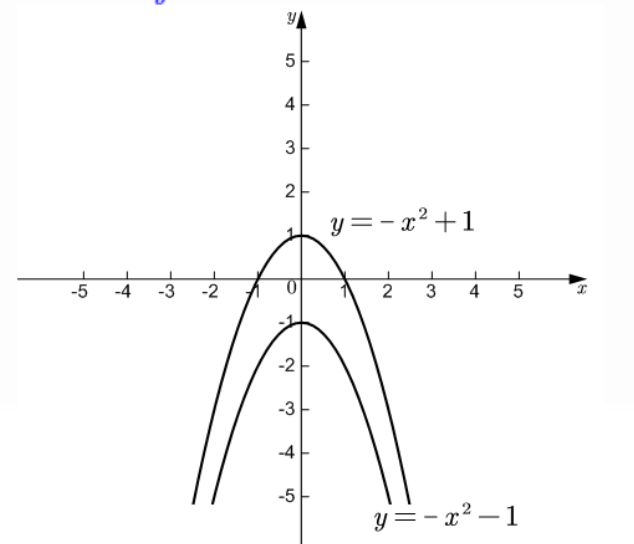
例 2 在同一平面直角坐标系中，分别画出二次函数 $ y = -x^{2} + 1 $ 与 $ y = -x^{2} - 1 $ 的图像，并结合图像说明怎样平移，可以由二次函数 $ y = -x^{2} + 1 $ 的图像得到二次函数 $ y = -x^{2} - 1 $ 的图像。