2. 如图,$ AD // BE // CF $,且 $ \frac{AB}{BC} = \frac{1}{2} $,则 $ \frac{EF}{DF} $ 等于 (
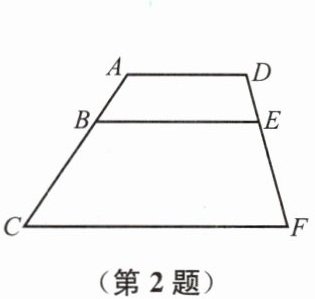
A.$ \frac{1}{2} $
B.$ \frac{2}{1} $
C.$ \frac{1}{3} $
D.$ \frac{2}{3} $
D
)
A.$ \frac{1}{2} $
B.$ \frac{2}{1} $
C.$ \frac{1}{3} $
D.$ \frac{2}{3} $
答案:D
3. 如图,$ DE // BC // FG $,图中的相似三角形有
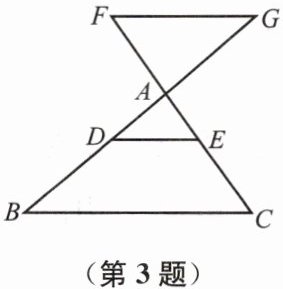
3
对.
答案:3
三、解答题
4. 如图,在 $ \triangle ABC $ 中,$ DG // EH // FI // BC $.
(1) 已知 $ AD = 3 $,$ DF = 5 $,求 $ \frac{DG}{FI} $ 的值;
(2) 若 $ AD = DE = EF $,$ EH = 4 $,求 $ FI $ 的长.
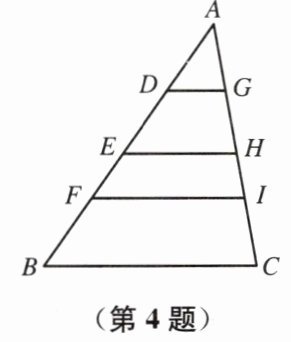
4. 如图,在 $ \triangle ABC $ 中,$ DG // EH // FI // BC $.
(1) 已知 $ AD = 3 $,$ DF = 5 $,求 $ \frac{DG}{FI} $ 的值;
(2) 若 $ AD = DE = EF $,$ EH = 4 $,求 $ FI $ 的长.

答案:解: (1)因为AD=3 , DF=5
所以AF=8
因为DG//FI
所以$\frac {DG}{FI}=\frac {AD}{AF}=\frac {3}{8}$
(2)因为AD=DE=EF
所以AE : AF=2: 3
因为EH//FI
所以$\frac {EH}{FI}=\frac {AE}{AF}=\frac {2}{3}$
因为EH=4
所以FI=6
所以AF=8
因为DG//FI
所以$\frac {DG}{FI}=\frac {AD}{AF}=\frac {3}{8}$
(2)因为AD=DE=EF
所以AE : AF=2: 3
因为EH//FI
所以$\frac {EH}{FI}=\frac {AE}{AF}=\frac {2}{3}$
因为EH=4
所以FI=6
5. 已知:如图,在正方形 $ ABCD $ 中,$ E $ 是边 $ BC $ 的延长线上的一点,连接 $ AE $ 交 $ CD $ 于点 $ F $,过点 $ F $ 作 $ FG // AD $,交 $ DE $ 于点 $ G $.
(1) 求证:$ CF = FG $;
(2) 试判断 $ FG $ 与 $ EG $ 的大小关系,并说明理由.
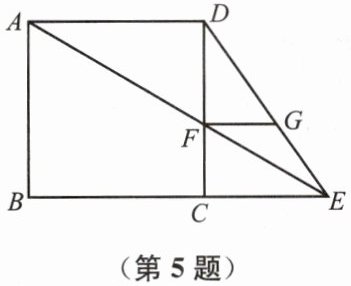
(1) 求证:$ CF = FG $;
(2) 试判断 $ FG $ 与 $ EG $ 的大小关系,并说明理由.

答案:解: (1)因为AD=3 , DF=5
所以AF=8
因为DG//FI
所以$\frac {DG}{FI}=\frac {AD}{AF}=\frac {3}{8}$
(2)因为AD=DE=EF
所以AE : AF=2: 3
因为EH//FI
所以$\frac {EH}{FI}=\frac {AE}{AF}=\frac {2}{3}$
因为EH=4
所以FI=6
证明:因为FG//AD
所以$\frac {FG}{AD}=\frac {EG}{ED}$
因为四边形ABCD是正方形.
所以AD=CD , AD//BC
因为FG//AD
所以FG∥BC
所以$\frac {EG}{ED}=\frac {CF}{CD}$
所以$\frac {FG}{AD}=\frac {CF}{CD}$
因为AD=CD
所以CF=FG
所以AF=8
因为DG//FI
所以$\frac {DG}{FI}=\frac {AD}{AF}=\frac {3}{8}$
(2)因为AD=DE=EF
所以AE : AF=2: 3
因为EH//FI
所以$\frac {EH}{FI}=\frac {AE}{AF}=\frac {2}{3}$
因为EH=4
所以FI=6
证明:因为FG//AD
所以$\frac {FG}{AD}=\frac {EG}{ED}$
因为四边形ABCD是正方形.
所以AD=CD , AD//BC
因为FG//AD
所以FG∥BC
所以$\frac {EG}{ED}=\frac {CF}{CD}$
所以$\frac {FG}{AD}=\frac {CF}{CD}$
因为AD=CD
所以CF=FG