4. 已知:如图,在四边形 ABCD 中,AD//BC,∠A=90°,BD⊥CD.
求证:△ABD∽△DCB.

求证:△ABD∽△DCB.

答案:证明:因为AD//BC
所以∠ADB=∠DBC
因为∠A=90°, BD⊥CD
所以∠A=∠BDC= 90°
因为∠ADB=∠DBC,∠A=∠BDC
所以△ABD∽△DCB
所以∠ADB=∠DBC
因为∠A=90°, BD⊥CD
所以∠A=∠BDC= 90°
因为∠ADB=∠DBC,∠A=∠BDC
所以△ABD∽△DCB
5. 已知:如图,AB 是⊙O 的弦,直径 CD⊥AB,E 是 AB 延长线上的一点,CE 交⊙O 于点 F.
求证:$AC^{2}=CE· CF$.

求证:$AC^{2}=CE· CF$.

答案:证明:连结CB,BF,DF
因为直径CD⊥AB
所以AC= BC
因为CD是直径
所以∠CFD= 90°
所以∠D=90°-∠DCF=∠E
所以∠CBF=∠D=∠E,
又∠BCF=∠ECB
所以△BCF∽△ECB
所以$\frac {BC}{CF}=\frac {BC}{EC}$
所以BC²= CE×CF,
又AC= BC
所以AC²= CE×CF
因为直径CD⊥AB
所以AC= BC
因为CD是直径
所以∠CFD= 90°
所以∠D=90°-∠DCF=∠E
所以∠CBF=∠D=∠E,
又∠BCF=∠ECB
所以△BCF∽△ECB
所以$\frac {BC}{CF}=\frac {BC}{EC}$
所以BC²= CE×CF,
又AC= BC
所以AC²= CE×CF
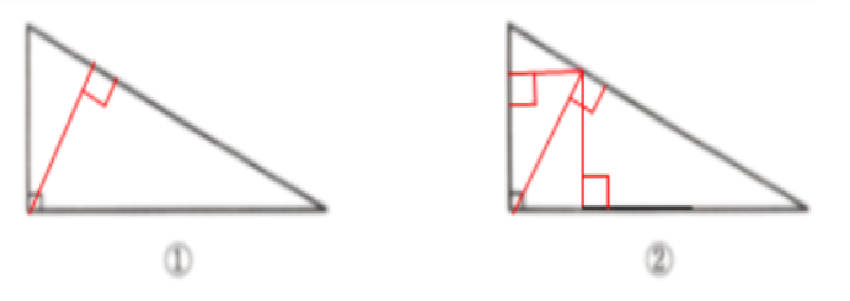
6. (1) 你能将一个直角三角形分成两个三角形,并且使它们都与原三角形相似吗? 试试看,在图①中画出你的设计方案.
(2) 如果要将这个直角三角形分割成 4 个三角形,并且使它们仍然都与原三角形相似,你还能做到吗? 在图②中画画看.

(2) 如果要将这个直角三角形分割成 4 个三角形,并且使它们仍然都与原三角形相似,你还能做到吗? 在图②中画画看.

答案: