例 1 在$\triangle ABC$和$\triangle A'B'C'$中,$AB = 2$,$BC = 4$,$AC = 3$,$A'B' = 3$,$B'C' = 6$,$A'C' = 4.5$.$\triangle ABC$与$\triangle A'B'C'$相似吗?为什么?
答案:解:相似,理由如下:
因为AB=2 , BC=4,AC=3 ,
A'B'=3 , B'C'=6 , A'C'=4.5 .
所以$\frac {AB}{A'B'}=\frac {BC}{B'C'}=\frac {AC}{A'C'}=\frac {2}{3}$
所以△ABC∽△A'B'C'
因为AB=2 , BC=4,AC=3 ,
A'B'=3 , B'C'=6 , A'C'=4.5 .
所以$\frac {AB}{A'B'}=\frac {BC}{B'C'}=\frac {AC}{A'C'}=\frac {2}{3}$
所以△ABC∽△A'B'C'
例 2 如图 6.4.7,在正方形网格上有$\triangle A_1B_1C_1$和$\triangle A_2B_2C_2$,这两个三角形相似吗?请说明你的理由.
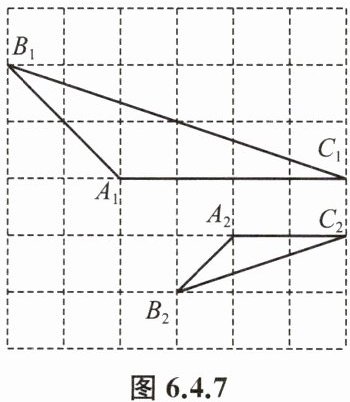

答案:解:相似,理由如下:
由图可知,$A_{1}B_{1}=\sqrt{2²+2²}= 2\sqrt{2},$
$A_{2}B_{2}=\sqrt{1²+1²}=\sqrt{2},$
$ A_{1}C_{1}=4,$$ A_{2}C_{2}= 2,$
$B_{1}C_{1}=\sqrt{2²+6²}=2\sqrt{10}$
$B_{2}C_{2}=\sqrt{1²+3²}=\sqrt{10}$
因为$\frac {A_{1}B_{1}}{A_{2}B_{2}}=\frac {A_{1}C_{1}}{A_{2}C_{2}}=\frac {B_{1}C_{1}}{B_{2}C_{2}}$
所以$△A_{1}B_{1}C_{1}∽△A_{2}B_{2}C_{2}$
由图可知,$A_{1}B_{1}=\sqrt{2²+2²}= 2\sqrt{2},$
$A_{2}B_{2}=\sqrt{1²+1²}=\sqrt{2},$
$ A_{1}C_{1}=4,$$ A_{2}C_{2}= 2,$
$B_{1}C_{1}=\sqrt{2²+6²}=2\sqrt{10}$
$B_{2}C_{2}=\sqrt{1²+3²}=\sqrt{10}$
因为$\frac {A_{1}B_{1}}{A_{2}B_{2}}=\frac {A_{1}C_{1}}{A_{2}C_{2}}=\frac {B_{1}C_{1}}{B_{2}C_{2}}$
所以$△A_{1}B_{1}C_{1}∽△A_{2}B_{2}C_{2}$
1. 在$\triangle ABC$和$\triangle DEF$中,$AB = 4\ \mathrm{cm}$,$BC = 5\ \mathrm{cm}$,$AC = 8\ \mathrm{cm}$,$DE = \frac{5}{3}\ \mathrm{cm}$,$DF = \frac{10}{3}\ \mathrm{cm}$,则$EF =$
$\frac{25}{12}$
时,$\triangle ABC \backsim \triangle DEF$.答案:$\frac {25}{12}\ \mathrm {cm}$
2. 如图,已知$M$为$\triangle ABC$的重心,则$\frac{AM}{DM}$的值为
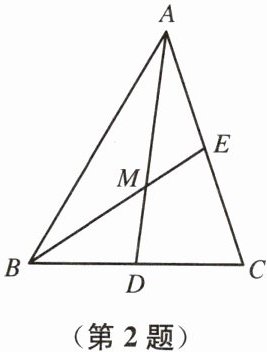
2
.
答案:2
3. 小张要制作两个形状完全相同的三角形框架.其中一个三角形框架三边长分别是$20\ \mathrm{cm}$、$24\ \mathrm{cm}$、$28\ \mathrm{cm}$,另一个三角形框架的最长边为$21\ \mathrm{cm}$,在截料时(不考虑其他因素),另两边应该截成
15
$\mathrm{cm}$和18
$\mathrm{cm}$.答案:15
18
18