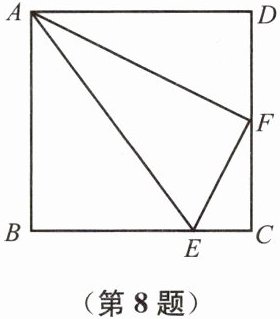
8. 如图,在正方形$ABCD$中,$BE = 3CE$,$CF = DF$.
求证:(1)$AE^2 = AF^2 + EF^2$;(2)$\triangle AEF \backsim \triangle AFD$.
求证:(1)$AE^2 = AF^2 + EF^2$;(2)$\triangle AEF \backsim \triangle AFD$.

答案:证明:(1)设正方形边长为4x ,
则CF= DF= 2x,BE= 3x, CE= x
AE²=AB²+BE²=16x²+ 9x²= 25x²
AF²+ EF²= AD²+DF²+FC²+EC²=16x²+4x²+4x²+x²= 25x²
所以AE²= AF²+ EF²
(2)由(1)AE= 5x,$ AF= 2\sqrt{5}x ,$$ EF=\sqrt{5}x$
AD= 4x,DF= 2x
所以$\frac {AE}{AF}=\frac {AF}{AD}=\frac {EF}{DF}=\frac {\sqrt{5}}{2}$
所以△AEF∽△AFD
则CF= DF= 2x,BE= 3x, CE= x
AE²=AB²+BE²=16x²+ 9x²= 25x²
AF²+ EF²= AD²+DF²+FC²+EC²=16x²+4x²+4x²+x²= 25x²
所以AE²= AF²+ EF²
(2)由(1)AE= 5x,$ AF= 2\sqrt{5}x ,$$ EF=\sqrt{5}x$
AD= 4x,DF= 2x
所以$\frac {AE}{AF}=\frac {AF}{AD}=\frac {EF}{DF}=\frac {\sqrt{5}}{2}$
所以△AEF∽△AFD
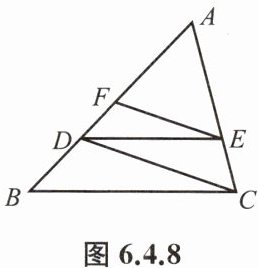
例1 已知:如图6.4.8,DE//BC,EF//DC.
求证:AD²=AF·AB.
求证:AD²=AF·AB.

答案:证明:因为DE//BC
所以$\frac {AD}{AB}=\frac {AE}{AC}$
因为EF//DC
所以$\frac {AF}{AD}=\frac {AE}{AC}$
所以$\frac {AD}{AB}=\frac {AF}{AD}$
所以AD²= AF×AB
所以$\frac {AD}{AB}=\frac {AE}{AC}$
因为EF//DC
所以$\frac {AF}{AD}=\frac {AE}{AC}$
所以$\frac {AD}{AB}=\frac {AF}{AD}$
所以AD²= AF×AB
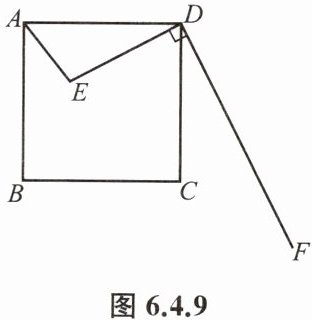
例2 如图6.4.9,已知E是边长为4的正方形ABCD内一点,且DE=3,DF⊥DE,垂足为D.在射线DF上是否存在这样的点M,使得以C、D、M为顶点的三角形与△ADE相似?若存在,请求出满足条件的DM的长;若不存在,请说明理由.

答案:解:存在
因为正方形ABCD的边长为$4\ \mathrm {cm}$
所以$AD=CD=4\ \mathrm {cm},$∠ADC= 90°
因为DF⊥DE
所以∠EDF=90°
所以∠ADE=∠CDF
①当$\frac {AD}{CD}=\frac {DE}{DM}$时, △ADE∽△CDM
因为$AD=CD=4\ \mathrm {cm},$$DE=3\ \mathrm {cm}$
所以$\frac {4}{4}=\frac {3}{DM}$
所以$DM= 3\ \mathrm {cm}$
②当$\frac {AD}{DM}=\frac {DE}{CD}$时,△ADE∽△CDM
因为$AD=CD=4\ \mathrm {cm},$$DE= 3\ \mathrm {cm}$
所以$\frac {4}{DM}=\frac {3}{4}$
所以$DM =\frac {16}{3}\ \mathrm {cm}$
综上所述,存在点M使得以C、D、M为顶点的三角形与△ADE
相似,此时DM的长为$3\ \mathrm {cm}$或$\frac {16}{3}\ \mathrm {cm}.$
因为正方形ABCD的边长为$4\ \mathrm {cm}$
所以$AD=CD=4\ \mathrm {cm},$∠ADC= 90°
因为DF⊥DE
所以∠EDF=90°
所以∠ADE=∠CDF
①当$\frac {AD}{CD}=\frac {DE}{DM}$时, △ADE∽△CDM
因为$AD=CD=4\ \mathrm {cm},$$DE=3\ \mathrm {cm}$
所以$\frac {4}{4}=\frac {3}{DM}$
所以$DM= 3\ \mathrm {cm}$
②当$\frac {AD}{DM}=\frac {DE}{CD}$时,△ADE∽△CDM
因为$AD=CD=4\ \mathrm {cm},$$DE= 3\ \mathrm {cm}$
所以$\frac {4}{DM}=\frac {3}{4}$
所以$DM =\frac {16}{3}\ \mathrm {cm}$
综上所述,存在点M使得以C、D、M为顶点的三角形与△ADE
相似,此时DM的长为$3\ \mathrm {cm}$或$\frac {16}{3}\ \mathrm {cm}.$