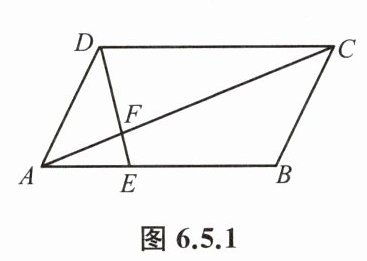
例2 如图6.5.1,在$□ ABCD$中,$E$为$AB$上一点,$DE$与$AC$相交于点$F$,若$AE:EB = 1:2$,且$\triangle AEF$的面积为$60\ \mathrm{cm}^2$.求$\triangle CDF$的面积.

答案:解:由平行四边形ABCD,得DC//AB,DC= AB
所以∠DCA=∠EAF,∠FDC= ∠FEA
所以△DCF∽△EAF,
由AE:EB=1:2,得AE:CD=1:3
所以$S_{△CDF} $:$ S_{△AEF}=1$:9
所以$S_{△CDF} = 540\ \mathrm {cm}²$
所以∠DCA=∠EAF,∠FDC= ∠FEA
所以△DCF∽△EAF,
由AE:EB=1:2,得AE:CD=1:3
所以$S_{△CDF} $:$ S_{△AEF}=1$:9
所以$S_{△CDF} = 540\ \mathrm {cm}²$
1. 若$\triangle ABC \backsim \triangle DEF$,且$AB = 2$,$DE = 3$,则$\triangle ABC$与$\triangle DEF$的周长之比为(
A.$2:3$
B.$3:2$
C.$4:9$
D.$9:4$
A
)A.$2:3$
B.$3:2$
C.$4:9$
D.$9:4$
答案:A
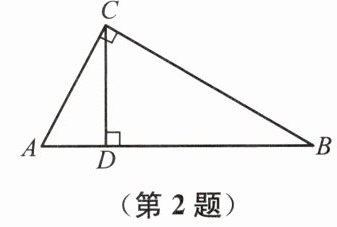
2. 如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CD ⊥ AB$,垂足为$D$,若$AC:BC = 1:2$,则$\triangle ADC$与$\triangle CDB$的面积之比为(
A.$1:2$
B.$1:3$
C.$1:4$
D.$1:5$
C
)
A.$1:2$
B.$1:3$
C.$1:4$
D.$1:5$
答案:C
3. 若两个相似五边形的面积比为$9:16$,其中较大的五边形的周长为$64\ \mathrm{cm}$,则较小的五边形的周长为
48
$\mathrm{cm}$.答案:48
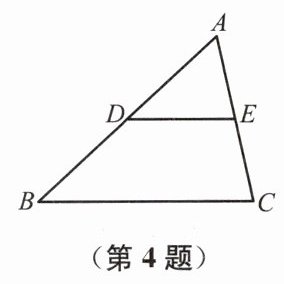
4. 如图,在$\triangle ABC$中,$D$、$E$分别是$AB$、$AC$的中点,那么$\triangle ADE$与四边形$DBCE$的面积之比是
1:3
.
答案:1:3
三、解答题
5. 已知$\triangle ABC \backsim \triangle DEF$,$AB$与$DE$的比为$3:2$,$\triangle ABC$与$\triangle DEF$的周长之差为$5\ \mathrm{cm}$.求$\triangle ABC$与$\triangle DEF$的周长之和.
5. 已知$\triangle ABC \backsim \triangle DEF$,$AB$与$DE$的比为$3:2$,$\triangle ABC$与$\triangle DEF$的周长之差为$5\ \mathrm{cm}$.求$\triangle ABC$与$\triangle DEF$的周长之和.
答案:解: 因为△ABC∽△DEF , AB与DE的比为3 : 2
所以△ABC与△DEF的周长之比为3 : 2
设△ABC的周长为$3x\ \mathrm {cm} ,$则△DEF的周长为$2x\ \mathrm {cm}$
因为△ABC与△DEF的周长相差$5\ \mathrm {cm}$
3x-2x=5
解得,x=5
所以△ABC的周长为$15\ \mathrm {cm} ,$ △DEF的周长为$10\ \mathrm {cm}$
所以△ABC和△DEF的周长之和为$25\ \mathrm {cm}$
所以△ABC与△DEF的周长之比为3 : 2
设△ABC的周长为$3x\ \mathrm {cm} ,$则△DEF的周长为$2x\ \mathrm {cm}$
因为△ABC与△DEF的周长相差$5\ \mathrm {cm}$
3x-2x=5
解得,x=5
所以△ABC的周长为$15\ \mathrm {cm} ,$ △DEF的周长为$10\ \mathrm {cm}$
所以△ABC和△DEF的周长之和为$25\ \mathrm {cm}$