3. 两个等腰直角三角形的周长分别为 5 cm、3 cm,它们的面积之比为
25:9
.答案:25:9
4. 两个相似三角形对应高之比为 3:5,这两个三角形的对应角平分线之比为
3:5
.答案:3:5
三、解答题
5. 如图,在四边形 ABCD 中,$\frac{BC}{CD}=\frac{3}{2}$,AC 平分∠BAD,∠ACB=∠ADC=90°,CF 和 DE 分别是△ABC、△ACD 的中线.求$\frac{CF}{DE}$的值.

5. 如图,在四边形 ABCD 中,$\frac{BC}{CD}=\frac{3}{2}$,AC 平分∠BAD,∠ACB=∠ADC=90°,CF 和 DE 分别是△ABC、△ACD 的中线.求$\frac{CF}{DE}$的值.

答案:解:由∠BAC=∠CAD,∠ACB=∠ADC= 90°
得△ABC∽△ACD
所以$\frac {AB}{AC}=\frac {BC}{CD}=\frac {3}{2}$
因为CF和DE分别是△ABC、ACD斜边上的中线
所以$CF=\frac {1}{2}AB,$$DE=\frac {1}{2}AC,$
所以$\frac {CF}{DE}=\frac {AB}{BC}=\frac {3}{2}$
得△ABC∽△ACD
所以$\frac {AB}{AC}=\frac {BC}{CD}=\frac {3}{2}$
因为CF和DE分别是△ABC、ACD斜边上的中线
所以$CF=\frac {1}{2}AB,$$DE=\frac {1}{2}AC,$
所以$\frac {CF}{DE}=\frac {AB}{BC}=\frac {3}{2}$
6. 如图,把△ABC 沿边 AB 平移到△A'B'C'的位置,它们重叠区域(即图中的阴影部分)的面积是△ABC 的面积的一半.若 AB=$\sqrt{2}$,求此三角形移动的距离AA'的长.


答案:解:因为∠C'A'B= ∠CAB,∠C'BA'=∠CBA
所以△ABC与阴影部分的三角形相似
因为阴影部分面积是△ABC的面积的一半,
所以AB:$ A'B=\sqrt{2}$: 1
所以A'B= 1,
所以$AA' =\sqrt{2}-1$
所以△ABC与阴影部分的三角形相似
因为阴影部分面积是△ABC的面积的一半,
所以AB:$ A'B=\sqrt{2}$: 1
所以A'B= 1,
所以$AA' =\sqrt{2}-1$
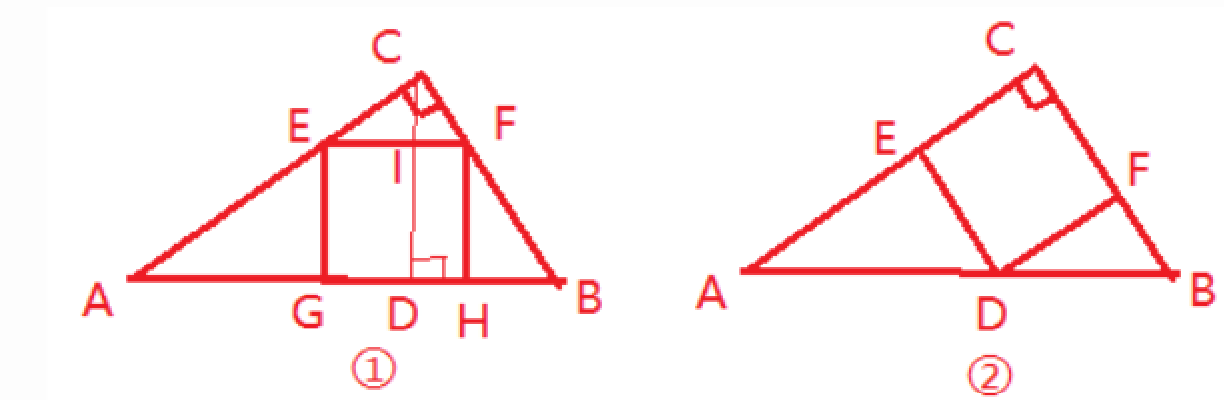
7. 如图是一块直角三角形板材,其中,∠C=90°,AC=8 cm,BC=6 cm.如何从这块板材上裁剪下一块面积最大的正方形? 请画出你的设计图,并求出这块正方形的边长.


答案:
解:①如图①, EF//AB
所以$\frac {EF}{AB}=\frac {CI}{CD}$
$AB=\sqrt{8²+6²}= 10,$$ CD=\frac {8×6}{10}= 4.8$
设正方形边长为:$x\ \mathrm {cm} ,$
$\frac {x}{10}=\frac {4.8}{4}-8,$
解得$x= \frac {120}{37}$
②如图②,可得△AED∽△DFB∽△ACB
设正方形边长为$n\ \mathrm {cm}$
则$AD=\frac {5}{3}n,$$BD=\frac {5}{4}n$
$AB=\frac {5}{3}n+\frac {5}{4}n=10$
解得$n=\frac {24}{7}$
$\frac {120}{37}≈3.2;$$\frac {24}{7}≈3.4$
所以$\frac {24}{7}>\frac {120}{37}$
所以图②中正方形即为所求,边长为$\frac {24}{7}$
解:①如图①, EF//AB
所以$\frac {EF}{AB}=\frac {CI}{CD}$
$AB=\sqrt{8²+6²}= 10,$$ CD=\frac {8×6}{10}= 4.8$
设正方形边长为:$x\ \mathrm {cm} ,$
$\frac {x}{10}=\frac {4.8}{4}-8,$
解得$x= \frac {120}{37}$
②如图②,可得△AED∽△DFB∽△ACB
设正方形边长为$n\ \mathrm {cm}$
则$AD=\frac {5}{3}n,$$BD=\frac {5}{4}n$
$AB=\frac {5}{3}n+\frac {5}{4}n=10$
解得$n=\frac {24}{7}$
$\frac {120}{37}≈3.2;$$\frac {24}{7}≈3.4$
所以$\frac {24}{7}>\frac {120}{37}$
所以图②中正方形即为所求,边长为$\frac {24}{7}$
