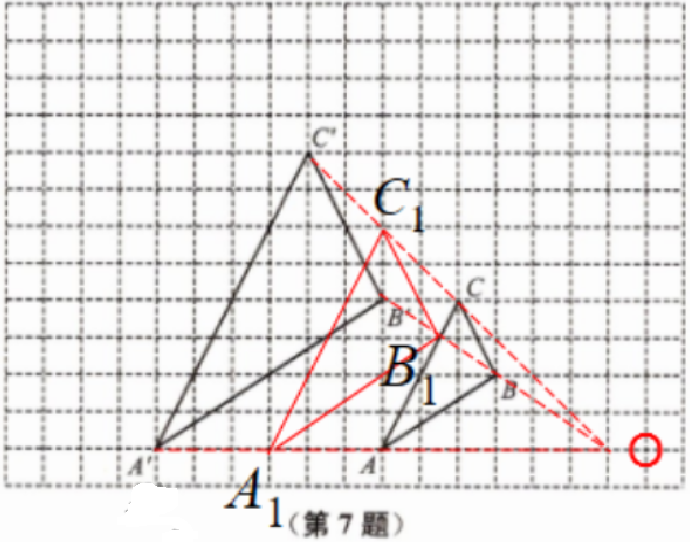
7. 如图,每个小方格都是边长为 1 的正方形,△ABC 与△A'B'C'是位似图形,它们的顶点都在小正方形的顶点上.
(1)画出△ABC 与△A'B'C'的位似中心 O;
(2)以点 O 为位似中心,画一个△A₁B₁C₁,使它与△ABC 的相似比等于 1.5.

(1)画出△ABC 与△A'B'C'的位似中心 O;
(2)以点 O 为位似中心,画一个△A₁B₁C₁,使它与△ABC 的相似比等于 1.5.

答案:

8. 如图,用下面的方法可以画△AOB 的“内接等边三角形”,阅读后对相应的问题做出说明.
画法:(1)在△AOB 内画等边三角形 CDE,使点 C 在 OA 上,点 D 在 OB 上;
(2)连接 OE 并延长,交 AB 于点 E',过点 E'作 E'C'//EC,交 OA 于点 C',作 E'D'//ED,交 OB 于点 D';(3)连接 C'D',△C'D'E'是△AOB 的内接三角形.
请你判断△C'D'E'是否是等边三角形,并说明理由.

画法:(1)在△AOB 内画等边三角形 CDE,使点 C 在 OA 上,点 D 在 OB 上;
(2)连接 OE 并延长,交 AB 于点 E',过点 E'作 E'C'//EC,交 OA 于点 C',作 E'D'//ED,交 OB 于点 D';(3)连接 C'D',△C'D'E'是△AOB 的内接三角形.
请你判断△C'D'E'是否是等边三角形,并说明理由.

答案:解:△C'D'E'是等边三角形,理由如下:
因为E'C'//EC , E'D'//ED , △CDE为等边三角形
所以△OCE∽△OC'E', △ODE∽△OD'E',
∠C'E'D'=∠CED= 60°
所以$\frac {CE}{C'E'}=\frac {OE}{OE'},$$\frac {DE}{D'E'}=\frac {OE}{OE'}$
所以$\frac {CE}{C'E'}=\frac {DE}{D'E'}$
因为∠C'E'D'=∠CED
所以△CDE∽△C'D'E'
所以△C'D'E'是等边三角形
因为E'C'//EC , E'D'//ED , △CDE为等边三角形
所以△OCE∽△OC'E', △ODE∽△OD'E',
∠C'E'D'=∠CED= 60°
所以$\frac {CE}{C'E'}=\frac {OE}{OE'},$$\frac {DE}{D'E'}=\frac {OE}{OE'}$
所以$\frac {CE}{C'E'}=\frac {DE}{D'E'}$
因为∠C'E'D'=∠CED
所以△CDE∽△C'D'E'
所以△C'D'E'是等边三角形