2. 如图,身高 $1.6$ m 的小华($CE$)站在距灯杆 $AB$ $5$ m 的点 $C$ 处,测得她在灯光下的影长 $CD$ 为 $2.5$ m,则灯杆 $AB$ 的高度为

4.8
m.
答案:4.8
3. 如图,设小孔 $O$ 前 $24$ cm 处有一支长 $18.6$ cm 的蜡烛 $AB$ 经小孔 $O$ 成像,在小孔 $O$ 后面 $10$ cm 的屏幕上所成像 $A'B'$ 的长是

$\frac{31}{4}$
cm.
答案:3.$\frac{31}{4}$.
解析:
解:由小孔成像原理知,$\triangle AOB \sim \triangle A'OB'$。
设像$A'B'$的长为$x$ cm,根据相似三角形对应边成比例,可得:
$\frac{AB}{A'B'} = \frac{24}{10}$
即$\frac{18.6}{x} = \frac{24}{10}$
解得$x = \frac{18.6 × 10}{24} = \frac{186}{24} = \frac{31}{4}$
$\frac{31}{4}$
设像$A'B'$的长为$x$ cm,根据相似三角形对应边成比例,可得:
$\frac{AB}{A'B'} = \frac{24}{10}$
即$\frac{18.6}{x} = \frac{24}{10}$
解得$x = \frac{18.6 × 10}{24} = \frac{186}{24} = \frac{31}{4}$
$\frac{31}{4}$
4. 《九章算术》中记载了一种测量井深的方法. 如图,在井口 $B$ 处立一根垂直于井口的木杆 $BD$,从木杆的顶端 $D$ 观察井水水面 $C$,视线 $DC$ 与井口的直径 $AB$ 交于点 $E$. 如果测得 $AB = 1$ m,$BD = 1.5$ m,$BE = 0.2$ m,那么井深 $AC$ 为

6
m.
答案:7.75
6
6
三、解答题
5. 如图,小芳在打网球时,她的击球高度是 $2.4$ m,为使球恰好能过网(网高为 $0.9$ m),且落在对方区域距离网 $4.8$ m 的位置,若网球的运动轨迹可看作一条直线,则她应站在离网多远处?

5. 如图,小芳在打网球时,她的击球高度是 $2.4$ m,为使球恰好能过网(网高为 $0.9$ m),且落在对方区域距离网 $4.8$ m 的位置,若网球的运动轨迹可看作一条直线,则她应站在离网多远处?

答案:解:设她应站在离网x米处,即BD=xm。
由题意得, AB//CD
所以△OAB∽△OCD
所以$\frac {AB}{CD}=\frac {OB}{OD}$
因为AB=0.9m,CD=2.4m , OB=4.8m,OD=OB+BD=(4.8+x)m
所以$\frac {0.9}{2.4}=\frac {4.8}{4.8+x}$
解得,x=8
所以BD= 8m
答:她应站在离网8米远处。
由题意得, AB//CD
所以△OAB∽△OCD
所以$\frac {AB}{CD}=\frac {OB}{OD}$
因为AB=0.9m,CD=2.4m , OB=4.8m,OD=OB+BD=(4.8+x)m
所以$\frac {0.9}{2.4}=\frac {4.8}{4.8+x}$
解得,x=8
所以BD= 8m
答:她应站在离网8米远处。
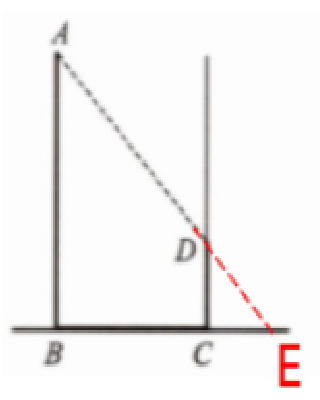
6. 课外学习小组想利用树影测量树高,他们在同一时刻测得一身高为 $1.5$ m 的同学的影长为 $1.35$ m,因大树靠近一幢建筑物,影子并未全部落在地面上(如图),现测得地面上树影的长 $BC = 3.6$ m,墙面上树影的高 $CD = 1.8$ m. 求树高 $AB$.


答案:
解:延长AD ,与直线BC交于点E ,如图所示
因为AB//CD
所以△CDE∽△BAE
所以$\frac {CD}{CE}=\frac {AB}{BE}=\frac {1.5}{1.35}$
因为CD=1.8m . CE=1.62m
因为BC=3.6m
所以BE= BC+CE= 5.22m
因为$\frac {AB}{BE}=\frac {1.5}{1.35}$
所以AB=5.8m
答:树高AB为5.8m
解:延长AD ,与直线BC交于点E ,如图所示
因为AB//CD
所以△CDE∽△BAE
所以$\frac {CD}{CE}=\frac {AB}{BE}=\frac {1.5}{1.35}$
因为CD=1.8m . CE=1.62m
因为BC=3.6m
所以BE= BC+CE= 5.22m
因为$\frac {AB}{BE}=\frac {1.5}{1.35}$
所以AB=5.8m
答:树高AB为5.8m
