7. 如图,工地上竖立着两根电线杆 AB、CD.现分别自两杆上的点 A、C 处向两侧地面上的点 E、D 和点 B、F 引钢丝绳并拉紧,以固定电线杆.已知 AB=4 m,CD=6 m,求钢丝绳 AD 与 BC 的交点 P 离地面的高度.


答案:
解:过点P作PG⊥EF ,垂足为点G ,如图所示
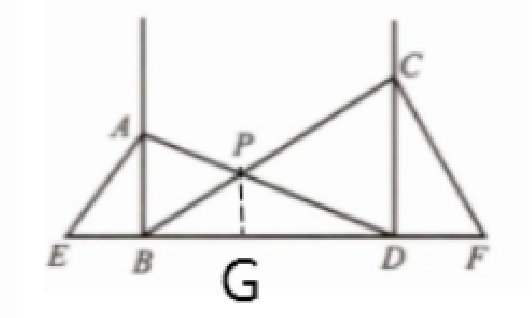
由题意得, AB//CD//PG
因为AB//PG
所以△PGD∽△ABD
所以$\frac {PG}{AB}=\frac {DG}{DB}$
因为CD//PG
所以△PGB∽△CDB,
所以$\frac {PG}{CD}=\frac {GB}{DB}$
因为$\frac {DG}{DB}+\frac {GB}{DB}=\frac {DB}{DB}=1$
所以$\frac {PG}{AB}+\frac {PG}{CD}=1$
因为AB=4m,CD=6m
所以$\frac {PG}{4}+\frac {PG}{6}=1$
所以$PG=\frac {12}{5}m$
答:交点P离地面的高度为$\frac {12}{5}m$
解:过点P作PG⊥EF ,垂足为点G ,如图所示

由题意得, AB//CD//PG
因为AB//PG
所以△PGD∽△ABD
所以$\frac {PG}{AB}=\frac {DG}{DB}$
因为CD//PG
所以△PGB∽△CDB,
所以$\frac {PG}{CD}=\frac {GB}{DB}$
因为$\frac {DG}{DB}+\frac {GB}{DB}=\frac {DB}{DB}=1$
所以$\frac {PG}{AB}+\frac {PG}{CD}=1$
因为AB=4m,CD=6m
所以$\frac {PG}{4}+\frac {PG}{6}=1$
所以$PG=\frac {12}{5}m$
答:交点P离地面的高度为$\frac {12}{5}m$
1. 长度如下的四条线段中,成比例的是(
A.$1\ \mathrm{cm},2\ \mathrm{cm},3\ \mathrm{cm},4\ \mathrm{cm}$
B.$1.5\ \mathrm{cm},2.5\ \mathrm{cm},4.5\ \mathrm{cm},6.5\ \mathrm{cm}$
C.$\sqrt{2}\ \mathrm{cm},\sqrt{3}\ \mathrm{cm},\sqrt{5}\ \mathrm{cm},\frac{\sqrt{30}}{2}\ \mathrm{cm}$
D.$3\ \mathrm{cm},4\ \mathrm{cm},5\ \mathrm{cm},6\ \mathrm{cm}$
C
)A.$1\ \mathrm{cm},2\ \mathrm{cm},3\ \mathrm{cm},4\ \mathrm{cm}$
B.$1.5\ \mathrm{cm},2.5\ \mathrm{cm},4.5\ \mathrm{cm},6.5\ \mathrm{cm}$
C.$\sqrt{2}\ \mathrm{cm},\sqrt{3}\ \mathrm{cm},\sqrt{5}\ \mathrm{cm},\frac{\sqrt{30}}{2}\ \mathrm{cm}$
D.$3\ \mathrm{cm},4\ \mathrm{cm},5\ \mathrm{cm},6\ \mathrm{cm}$
答案:C
2. 在下列所给的条件中,能判定$\triangle ABC\backsim\triangle A'B'C'$的是(
A.$AB=\frac{3}{2},BC = 6,A'B' = 16,B'C' = 12,\angle A=\angle A'$
B.$\angle A = 70^{\circ},\angle B = 35^{\circ},\angle A' = 70^{\circ},\angle C' = 85^{\circ}$
C.$AB = 4,BC = 6,AC = 8,A'B' = 12,B'C' = 18,A'C' = 24$
D.$\angle C=\angle C' = 90^{\circ},AB = 15,AC = 5,A'B' = 5,B'C'=\frac{5}{3}$
C
)A.$AB=\frac{3}{2},BC = 6,A'B' = 16,B'C' = 12,\angle A=\angle A'$
B.$\angle A = 70^{\circ},\angle B = 35^{\circ},\angle A' = 70^{\circ},\angle C' = 85^{\circ}$
C.$AB = 4,BC = 6,AC = 8,A'B' = 12,B'C' = 18,A'C' = 24$
D.$\angle C=\angle C' = 90^{\circ},AB = 15,AC = 5,A'B' = 5,B'C'=\frac{5}{3}$
答案:C
3. 如图,$DE// BC,EF// AB$,则(

A.$\frac{AD}{DB}=\frac{DE}{BC}$
B.$\frac{AD}{DB}=\frac{DE}{FC}$
C.$\frac{AE}{EC}=\frac{DE}{BC}$
D.$\frac{EF}{AB}=\frac{CF}{FB}$
B
)
A.$\frac{AD}{DB}=\frac{DE}{BC}$
B.$\frac{AD}{DB}=\frac{DE}{FC}$
C.$\frac{AE}{EC}=\frac{DE}{BC}$
D.$\frac{EF}{AB}=\frac{CF}{FB}$
答案:3.B.
解析:
证明:
∵ $DE // BC$,
∴ $\triangle ADE \sim \triangle ABC$,$\frac{AD}{AB} = \frac{DE}{BC}$,$\frac{AD}{DB} = \frac{AE}{EC}$。
∵ $EF // AB$,
∴ 四边形 $BDEF$ 是平行四边形,$DE = BF$;
$\triangle EFC \sim \triangle ABC$,$\frac{AE}{EC} = \frac{BF}{FC}$。
∵ $\frac{AD}{DB} = \frac{AE}{EC}$ 且 $\frac{AE}{EC} = \frac{BF}{FC}$,$DE = BF$,
∴ $\frac{AD}{DB} = \frac{DE}{FC}$。
结论:B.
∵ $DE // BC$,
∴ $\triangle ADE \sim \triangle ABC$,$\frac{AD}{AB} = \frac{DE}{BC}$,$\frac{AD}{DB} = \frac{AE}{EC}$。
∵ $EF // AB$,
∴ 四边形 $BDEF$ 是平行四边形,$DE = BF$;
$\triangle EFC \sim \triangle ABC$,$\frac{AE}{EC} = \frac{BF}{FC}$。
∵ $\frac{AD}{DB} = \frac{AE}{EC}$ 且 $\frac{AE}{EC} = \frac{BF}{FC}$,$DE = BF$,
∴ $\frac{AD}{DB} = \frac{DE}{FC}$。
结论:B.