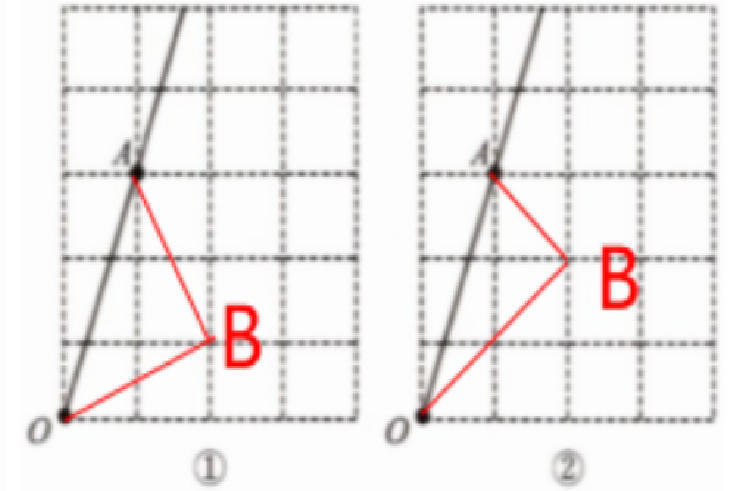
例 2 如图 7.1.2,射线 $ OA $ 在 $ 4 × 5 $ 的正方形网格中,点 $ O $、$ A $ 在格点上,请你分别在图①、图②中再找出格点 $ B $,连接 $ OB $、$ AB $,使 $ \triangle AOB $ 为直角三角形,并且满足:
(1)图①中的 $ \tan \angle AOB $ 的值为 $ 1 $;
(2)图②中的 $ \tan \angle AOB $ 的值为 $ \dfrac{1}{2} $.

(1)图①中的 $ \tan \angle AOB $ 的值为 $ 1 $;
(2)图②中的 $ \tan \angle AOB $ 的值为 $ \dfrac{1}{2} $.

答案:

1. 在 $ \mathrm{Rt} \triangle ABC $ 中,$ \angle ABC = 90^{\circ} $,$ AB = 5 $,$ BC = 12 $,则 $ \tan A $ 的值为(
A.$ \dfrac{12}{13} $
B.$ \dfrac{12}{5} $
C.$ \dfrac{5}{13} $
D.$ \dfrac{5}{12} $
B
)A.$ \dfrac{12}{13} $
B.$ \dfrac{12}{5} $
C.$ \dfrac{5}{13} $
D.$ \dfrac{5}{12} $
答案:B
2. $ \tan 20^{\circ} $、$ \tan 50^{\circ} $、$ \tan 70^{\circ} $ 的大小关系正确的是(
A.$ \tan 70^{\circ} < \tan 50^{\circ} < \tan 20^{\circ} $
B.$ \tan 50^{\circ} < \tan 20^{\circ} < \tan 70^{\circ} $
C.$ \tan 20^{\circ} < \tan 50^{\circ} < \tan 70^{\circ} $
D.$ \tan 20^{\circ} < \tan 70^{\circ} < \tan 50^{\circ} $
C
)A.$ \tan 70^{\circ} < \tan 50^{\circ} < \tan 20^{\circ} $
B.$ \tan 50^{\circ} < \tan 20^{\circ} < \tan 70^{\circ} $
C.$ \tan 20^{\circ} < \tan 50^{\circ} < \tan 70^{\circ} $
D.$ \tan 20^{\circ} < \tan 70^{\circ} < \tan 50^{\circ} $
答案:2. C.
3. 在 $ \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ a : b = 3 : 5 $,则 $ \tan B = $
$\frac{5}{3}$
.答案:$\frac {5}{3}$
4. 在 $ \triangle ABC $ 中,$ \angle B = 90^{\circ} $,$ AC = \sqrt{5} $,$ \tan C = 2 $,则 $ BC $ 的长为
1
.答案:1. 首先,根据三角函数的定义:
在$Rt\triangle ABC$中,$\angle B = 90^{\circ}$,$\tan C=\frac{AB}{BC}$,已知$\tan C = 2$,设$BC=x$,则$AB = 2x$。
2. 然后,根据勾股定理:
勾股定理公式为$AB^{2}+BC^{2}=AC^{2}$。
已知$AC=\sqrt{5}$,将$AB = 2x$,$BC=x$代入勾股定理公式中,得到$(2x)^{2}+x^{2}=(\sqrt{5})^{2}$。
展开式子:
根据$(a + b)^2=a^{2}+2ab + b^{2}$,$(2x)^{2}=4x^{2}$,则$4x^{2}+x^{2}=5$。
合并同类项得$5x^{2}=5$。
求解$x$:
方程两边同时除以$5$,得$x^{2}=1$。
因为$x$是三角形的边长($x\gt0$),所以$x = 1$($x=-1$舍去)。
所以$BC$的长为$1$。
在$Rt\triangle ABC$中,$\angle B = 90^{\circ}$,$\tan C=\frac{AB}{BC}$,已知$\tan C = 2$,设$BC=x$,则$AB = 2x$。
2. 然后,根据勾股定理:
勾股定理公式为$AB^{2}+BC^{2}=AC^{2}$。
已知$AC=\sqrt{5}$,将$AB = 2x$,$BC=x$代入勾股定理公式中,得到$(2x)^{2}+x^{2}=(\sqrt{5})^{2}$。
展开式子:
根据$(a + b)^2=a^{2}+2ab + b^{2}$,$(2x)^{2}=4x^{2}$,则$4x^{2}+x^{2}=5$。
合并同类项得$5x^{2}=5$。
求解$x$:
方程两边同时除以$5$,得$x^{2}=1$。
因为$x$是三角形的边长($x\gt0$),所以$x = 1$($x=-1$舍去)。
所以$BC$的长为$1$。
5. 如图,在平面直角坐标系中,四边形 $ AOCB $ 为菱形,$ \tan \angle AOC = \dfrac{4}{3} $,且点 $ A $ 落在反比例函数 $ y = \dfrac{3}{x} $ 的图像上,点 $ B $ 落在反比例函数 $ y = \dfrac{k}{x} (k \neq 0) $ 的图像上,则 $ k = $

8
.
答案:5. 8.
解析:
解:设点$ A $的坐标为$ (a,b) $,因为点$ A $在反比例函数$ y = \dfrac{3}{x} $上,所以$ ab = 3 $。
过点$ A $作$ AD ⊥ x $轴于点$ D $,则$ OD = a $,$ AD = b $。
因为$ \tan \angle AOC = \dfrac{AD}{OD} = \dfrac{b}{a} = \dfrac{4}{3} $,所以$ b = \dfrac{4}{3}a $。
将$ b = \dfrac{4}{3}a $代入$ ab = 3 $,得$ a · \dfrac{4}{3}a = 3 $,即$ \dfrac{4}{3}a^2 = 3 $,解得$ a^2 = \dfrac{9}{4} $,$ a = \dfrac{3}{2} $($ a > 0 $),则$ b = \dfrac{4}{3} × \dfrac{3}{2} = 2 $,所以点$ A \left( \dfrac{3}{2}, 2 \right) $。
在$ \mathrm{Rt} \triangle AOD $中,$ OA = \sqrt{OD^2 + AD^2} = \sqrt{\left( \dfrac{3}{2} \right)^2 + 2^2} = \sqrt{\dfrac{9}{4} + 4} = \sqrt{\dfrac{25}{4}} = \dfrac{5}{2} $。
因为四边形$ AOCB $是菱形,所以$ BC = OA = \dfrac{5}{2} $,且$ BC // OA $。
设点$ C $的坐标为$ (c, 0) $,则$ OC = c $,$ OA = OC = \dfrac{5}{2} $,所以$ c = \dfrac{5}{2} $,即点$ C \left( \dfrac{5}{2}, 0 \right) $。
因为$ BC // OA $,且$ OA $的斜率为$ \dfrac{b}{a} = \dfrac{4}{3} $,所以$ BC $的斜率也为$ \dfrac{4}{3} $。
点$ B $的坐标为$ \left( c + \dfrac{3}{2}, 0 + 2 \right) = \left( \dfrac{5}{2} + \dfrac{3}{2}, 2 \right) = (4, 2) $。
因为点$ B $在反比例函数$ y = \dfrac{k}{x} $上,所以$ k = 4 × 2 = 8 $。
8
过点$ A $作$ AD ⊥ x $轴于点$ D $,则$ OD = a $,$ AD = b $。
因为$ \tan \angle AOC = \dfrac{AD}{OD} = \dfrac{b}{a} = \dfrac{4}{3} $,所以$ b = \dfrac{4}{3}a $。
将$ b = \dfrac{4}{3}a $代入$ ab = 3 $,得$ a · \dfrac{4}{3}a = 3 $,即$ \dfrac{4}{3}a^2 = 3 $,解得$ a^2 = \dfrac{9}{4} $,$ a = \dfrac{3}{2} $($ a > 0 $),则$ b = \dfrac{4}{3} × \dfrac{3}{2} = 2 $,所以点$ A \left( \dfrac{3}{2}, 2 \right) $。
在$ \mathrm{Rt} \triangle AOD $中,$ OA = \sqrt{OD^2 + AD^2} = \sqrt{\left( \dfrac{3}{2} \right)^2 + 2^2} = \sqrt{\dfrac{9}{4} + 4} = \sqrt{\dfrac{25}{4}} = \dfrac{5}{2} $。
因为四边形$ AOCB $是菱形,所以$ BC = OA = \dfrac{5}{2} $,且$ BC // OA $。
设点$ C $的坐标为$ (c, 0) $,则$ OC = c $,$ OA = OC = \dfrac{5}{2} $,所以$ c = \dfrac{5}{2} $,即点$ C \left( \dfrac{5}{2}, 0 \right) $。
因为$ BC // OA $,且$ OA $的斜率为$ \dfrac{b}{a} = \dfrac{4}{3} $,所以$ BC $的斜率也为$ \dfrac{4}{3} $。
点$ B $的坐标为$ \left( c + \dfrac{3}{2}, 0 + 2 \right) = \left( \dfrac{5}{2} + \dfrac{3}{2}, 2 \right) = (4, 2) $。
因为点$ B $在反比例函数$ y = \dfrac{k}{x} $上,所以$ k = 4 × 2 = 8 $。
8
三、解答题
6. 如图,$ \angle C = 90^{\circ} $,分别求出图中 $ \angle A $、$ \angle B $ 的正切值.

6. 如图,$ \angle C = 90^{\circ} $,分别求出图中 $ \angle A $、$ \angle B $ 的正切值.

答案:解:①在Rt△ABC中,
因为AC=12,BC=16
所以$AB=\sqrt{AC²+BC²}=20$
所以$tanA=\frac {BC}{AC}=\frac {16}{12}=\frac {4}{3}$
$tanB=\frac {AC}{BC}=\frac {12}{16}=\frac {3}{4}$
②在Rt△ABC中,
因为BC=8 ,$ AB=\sqrt{73}$
所以$AC=\sqrt{AB²-BC²}=3$
所以$tanA=\frac {BC}{AC}=\frac {8}{3},$$tanB=\frac {AC}{BC}=\frac {3}{8}$
解:①在Rt△ABC中,
因为AC=12,BC=16
所以$AB=\sqrt{AC²+BC²}=20$
所以$tanA=\frac {BC}{AC}=\frac {16}{12}=\frac {4}{3}$
$tanB=\frac {AC}{BC}=\frac {12}{16}=\frac {3}{4}$
②在Rt△ABC中,
因为BC=8 ,$ AB=\sqrt{73}$
所以$AC=\sqrt{AB²-BC²}=3$
所以$tanA=\frac {BC}{AC}=\frac {8}{3},$$tanB=\frac {AC}{BC}=\frac {3}{8}$
因为AC=12,BC=16
所以$AB=\sqrt{AC²+BC²}=20$
所以$tanA=\frac {BC}{AC}=\frac {16}{12}=\frac {4}{3}$
$tanB=\frac {AC}{BC}=\frac {12}{16}=\frac {3}{4}$
②在Rt△ABC中,
因为BC=8 ,$ AB=\sqrt{73}$
所以$AC=\sqrt{AB²-BC²}=3$
所以$tanA=\frac {BC}{AC}=\frac {8}{3},$$tanB=\frac {AC}{BC}=\frac {3}{8}$
解:①在Rt△ABC中,
因为AC=12,BC=16
所以$AB=\sqrt{AC²+BC²}=20$
所以$tanA=\frac {BC}{AC}=\frac {16}{12}=\frac {4}{3}$
$tanB=\frac {AC}{BC}=\frac {12}{16}=\frac {3}{4}$
②在Rt△ABC中,
因为BC=8 ,$ AB=\sqrt{73}$
所以$AC=\sqrt{AB²-BC²}=3$
所以$tanA=\frac {BC}{AC}=\frac {8}{3},$$tanB=\frac {AC}{BC}=\frac {3}{8}$