7. 如图,$ \triangle ABC $ 是锐角三角形,$ AB = 10 \mathrm{ cm} $,$ BC = 9 \mathrm{ cm} $,$ \triangle ABC $ 的面积为 $ 27 \mathrm{ cm}^2 $,求 $ \tan B $ 的值.


答案:
解:过点A作AD⊥BC于点D,
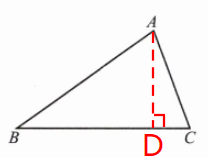
∵BC=9cm,$S_{△ABC}=\frac{1}{2}BC·AD=27cm^2$
∴AD=6cm
∵AB=10cm,AD⊥BC
∴$BD=\sqrt{AB^2-AD^2}=\sqrt{10^2-6^2}=8cm$
∴$tanB=\frac{AD}{BD}=\frac{6}{8}=\frac{3}{4}$
解:过点A作AD⊥BC于点D,

∵BC=9cm,$S_{△ABC}=\frac{1}{2}BC·AD=27cm^2$
∴AD=6cm
∵AB=10cm,AD⊥BC
∴$BD=\sqrt{AB^2-AD^2}=\sqrt{10^2-6^2}=8cm$
∴$tanB=\frac{AD}{BD}=\frac{6}{8}=\frac{3}{4}$
8. 如图,在正方形网格中,$ A $、$ B $、$ C $、$ D $ 四点都是格点,若 $ AB $、$ CD $ 相交于点 $ P $,则 $ \dfrac{AP}{PB} $ 的值为

3
,$ \tan \angle APD $ 的值为2
.
答案:3
2
2
9. 如图,过点 $ P $ 作 $ \odot O $ 的两条切线,切点分别为 $ A $、$ B $,连接 $ OA $、$ OB $、$ OP $,取 $ OP $ 的中点 $ C $,连接 $ AC $ 并延长,交 $ \odot O $ 于点 $ D $,连接 $ BD $.
(1)求证:$ \angle ADB = \angle AOP $.
(2)延长 $ OP $ 交 $ DB $ 的延长线于点 $ E $. 若 $ AP = 10 $,$ \tan \angle AOP = \dfrac{1}{2} $,求 $ DE $ 的长.

(1)求证:$ \angle ADB = \angle AOP $.
(2)延长 $ OP $ 交 $ DB $ 的延长线于点 $ E $. 若 $ AP = 10 $,$ \tan \angle AOP = \dfrac{1}{2} $,求 $ DE $ 的长.

答案:9. (1) 略;(2) 44.
解析:
(1) 证明:
∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,∠AOP=∠BOP。
∵C是OP中点,
∴AC=OC=PC,
∴∠OAC=∠AOP。
∵∠OAC=∠ADB(同弧所对圆周角相等),
∴∠ADB=∠AOP。
(2) 解:
在Rt△OAP中,tan∠AOP=AP/OA=1/2,AP=10,
∴OA=20,OP=√(OA²+AP²)=√(20²+10²)=10√5。
∵C是OP中点,
∴OC=PC=5√5。
由(1)知∠ADB=∠AOP,∠OAC=∠ADB,
∴∠OAC=∠AOP,
∴△OAC∽△ODA,
∴OA/OD=OC/OA,OD=OA²/OC=20²/(5√5)=16√5。
∵∠OBD=∠OAD=∠AOP,∠E=∠E,
∴△EBD∽△EOA,
∴EB/EO=BD/OA。
设OE=x,EB=y,
则BD=√(OD²-OB²)=√((16√5)²-20²)=24,
∴y/x=24/20=6/5,即y=6/5x。
在Rt△OBE中,OB²+EB²=OE²,
∴20²+(6/5x)²=x²,
解得x=50(负值舍去),
∴DE=OE+OD=50+16√5-16√5=44。
答案:(1) 见证明;(2) 44
∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,∠AOP=∠BOP。
∵C是OP中点,
∴AC=OC=PC,
∴∠OAC=∠AOP。
∵∠OAC=∠ADB(同弧所对圆周角相等),
∴∠ADB=∠AOP。
(2) 解:
在Rt△OAP中,tan∠AOP=AP/OA=1/2,AP=10,
∴OA=20,OP=√(OA²+AP²)=√(20²+10²)=10√5。
∵C是OP中点,
∴OC=PC=5√5。
由(1)知∠ADB=∠AOP,∠OAC=∠ADB,
∴∠OAC=∠AOP,
∴△OAC∽△ODA,
∴OA/OD=OC/OA,OD=OA²/OC=20²/(5√5)=16√5。
∵∠OBD=∠OAD=∠AOP,∠E=∠E,
∴△EBD∽△EOA,
∴EB/EO=BD/OA。
设OE=x,EB=y,
则BD=√(OD²-OB²)=√((16√5)²-20²)=24,
∴y/x=24/20=6/5,即y=6/5x。
在Rt△OBE中,OB²+EB²=OE²,
∴20²+(6/5x)²=x²,
解得x=50(负值舍去),
∴DE=OE+OD=50+16√5-16√5=44。
答案:(1) 见证明;(2) 44