例 1 计算:
(1)$\sin 30^{\circ}-\cos 60^{\circ}+\tan 45^{\circ}$;(2)$\frac{2\sin 60^{\circ}}{2-\tan 60^{\circ}}+\sqrt{(\cos 30^{\circ}-1)^{2}}$。
(1)$\sin 30^{\circ}-\cos 60^{\circ}+\tan 45^{\circ}$;(2)$\frac{2\sin 60^{\circ}}{2-\tan 60^{\circ}}+\sqrt{(\cos 30^{\circ}-1)^{2}}$。
答案:解:原式$=\frac {1}{2}-\frac {1}{2}+1$
=1
解:原式$=\frac {2×\frac {\sqrt{3}}{2}}{2-\sqrt{3}}+1-\frac {\sqrt{3}}{2} $
$ =\sqrt{3}×(2+\sqrt{3})+1-\frac {\sqrt{3}}{2} $
$ =4+\frac {3\sqrt{3}}{2} $
=1
解:原式$=\frac {2×\frac {\sqrt{3}}{2}}{2-\sqrt{3}}+1-\frac {\sqrt{3}}{2} $
$ =\sqrt{3}×(2+\sqrt{3})+1-\frac {\sqrt{3}}{2} $
$ =4+\frac {3\sqrt{3}}{2} $
例 2 如图 7.3.1,桔槔是一种原始的汲水工具,在一根竖立的架子上置一根细长的杠杆,末端悬挂重物,前端悬挂水桶,就制成了桔槔。当人把水桶放入水中打满水以后,由于杠杆末端的重力作用,把水提升至所需处比较省力。若已知杠杆 $AB = 6m$,$AO:OB = 2:1$,支架 $OM⊥ EF$,$OM = 3m$,$AB$ 可以绕着点 $O$ 自由旋转,当点 $A$ 旋转到如图所示位置时,$\angle AOM = 45^{\circ}$,求此时点 $B$ 到水平地面 $EF$ 的距离。


答案:
解:过点B作BD⊥EF{于} 点D,
过点A作AC⊥BD交BD于点C,
交OM于点N,
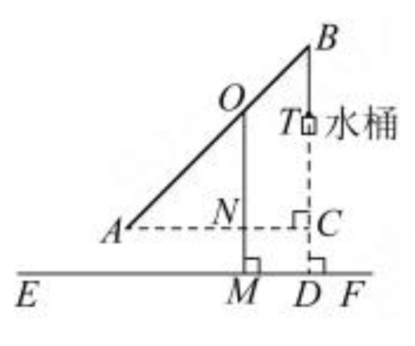
因为OM⊥EF,
所以OM//BC,.
所以AN⊥OM,
所以四边形MDCN为矩形,
所以MN= CD,
因为AB=6,AO:OB= 2:1,
所以$AO=\frac {2}{3}AB=4,$
在Rt△ANO中,AO=4,∠AOM= 45° ,
所以$ON=OA.cos_{45}° =4×\frac {\sqrt{2}}{2}= 2\sqrt{2} $
所以$CD= MN= OM- ON=3- 2\sqrt{2},$
在Rt△ACB中,AB=6,∠AOM = 45°
所以$BC=ABcos_{45}°=6×\frac {\sqrt{2}}{2}=3\sqrt{2}$
所以$BD=BC+CD=3\sqrt{2}+3-2\sqrt{2}=3+\sqrt{2}($米)
解:过点B作BD⊥EF{于} 点D,
过点A作AC⊥BD交BD于点C,
交OM于点N,

因为OM⊥EF,
所以OM//BC,.
所以AN⊥OM,
所以四边形MDCN为矩形,
所以MN= CD,
因为AB=6,AO:OB= 2:1,
所以$AO=\frac {2}{3}AB=4,$
在Rt△ANO中,AO=4,∠AOM= 45° ,
所以$ON=OA.cos_{45}° =4×\frac {\sqrt{2}}{2}= 2\sqrt{2} $
所以$CD= MN= OM- ON=3- 2\sqrt{2},$
在Rt△ACB中,AB=6,∠AOM = 45°
所以$BC=ABcos_{45}°=6×\frac {\sqrt{2}}{2}=3\sqrt{2}$
所以$BD=BC+CD=3\sqrt{2}+3-2\sqrt{2}=3+\sqrt{2}($米)
1. 若 $\sin\alpha=\cos\alpha$,则锐角 $\alpha$ 等于(
A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$75^{\circ}$
B
)A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$75^{\circ}$
答案:B
2. 点 $(-\sin 60^{\circ},\cos 60^{\circ})$ 关于 $y$ 轴对称的点的坐标是(
A.$(\frac{\sqrt{3}}{2},\frac{1}{2})$
B.$(-\frac{\sqrt{3}}{2},\frac{1}{2})$
C.$(-\frac{\sqrt{3}}{2},-\frac{1}{2})$
D.$(-\frac{1}{2},-\frac{\sqrt{3}}{2})$
A
)A.$(\frac{\sqrt{3}}{2},\frac{1}{2})$
B.$(-\frac{\sqrt{3}}{2},\frac{1}{2})$
C.$(-\frac{\sqrt{3}}{2},-\frac{1}{2})$
D.$(-\frac{1}{2},-\frac{\sqrt{3}}{2})$
答案:A
3. 计算:$\sin^{2}30^{\circ}+\cos^{2}30^{\circ}=$
1
;$\tan 45^{\circ}-\sqrt{2}\cos 45^{\circ}=$0
。答案:3. 1,0.
解析:
$\sin^{2}30^{\circ}+\cos^{2}30^{\circ}=\left(\frac{1}{2}\right)^{2}+\left(\frac{\sqrt{3}}{2}\right)^{2}=\frac{1}{4}+\frac{3}{4}=1$;$\tan 45^{\circ}-\sqrt{2}\cos 45^{\circ}=1-\sqrt{2}×\frac{\sqrt{2}}{2}=1 - 1=0$