4. 如图,一束光水平照射在有一定倾斜角度的平面镜上,若入射光线与反射光线的夹角为 $60^{\circ}$,则平面镜的垂线与水平地面的夹角 $\alpha$ 的余弦值为

$\frac{\sqrt{3}}{2}$
。
答案:$\frac {\sqrt{3}}{2}$
三、解答题
5. 计算:
(1)$2\cos 30^{\circ}+\tan 60^{\circ}-2\tan 45^{\circ}$;(2)$\sin^{2}45^{\circ}+\cos^{2}60^{\circ}$。
5. 计算:
(1)$2\cos 30^{\circ}+\tan 60^{\circ}-2\tan 45^{\circ}$;(2)$\sin^{2}45^{\circ}+\cos^{2}60^{\circ}$。
答案:5. (1) $2\sqrt{3}-2$;(2) $\frac{3}{4}$.
解析:
(1) $2\cos 30^{\circ}+\tan 60^{\circ}-2\tan 45^{\circ}$
$=2×\frac{\sqrt{3}}{2}+\sqrt{3}-2×1$
$=\sqrt{3}+\sqrt{3}-2$
$=2\sqrt{3}-2$
(2) $\sin^{2}45^{\circ}+\cos^{2}60^{\circ}$
$=\left(\frac{\sqrt{2}}{2}\right)^{2}+\left(\frac{1}{2}\right)^{2}$
$=\frac{2}{4}+\frac{1}{4}$
$=\frac{3}{4}$
$=2×\frac{\sqrt{3}}{2}+\sqrt{3}-2×1$
$=\sqrt{3}+\sqrt{3}-2$
$=2\sqrt{3}-2$
(2) $\sin^{2}45^{\circ}+\cos^{2}60^{\circ}$
$=\left(\frac{\sqrt{2}}{2}\right)^{2}+\left(\frac{1}{2}\right)^{2}$
$=\frac{2}{4}+\frac{1}{4}$
$=\frac{3}{4}$
6. 如图,以点 $O$ 为圆心,任意长为半径画弧,与射线 $OM$ 交于点 $A$,再以点 $A$ 为圆心,$AO$ 长为半径画弧,两弧交于点 $B$,画射线 $OB$,求 $\tan\angle AOB$ 的值。


答案:解:由题意得,OA=OB=AB
因为OA=OB=AB
所以△ABC是等边三角形
所以∠AOB= 60°
所以$tan∠AOB=\sqrt{3}$
因为OA=OB=AB
所以△ABC是等边三角形
所以∠AOB= 60°
所以$tan∠AOB=\sqrt{3}$
7. 如图,甲施工队沿 $AB$ 方向在一湖泊上架桥修路,为加快施工进度,乙施工队在湖另一边的点 $D$ 处同时施工。已知点 $D$ 在直线 $AB$ 上,且在点 $C$ 处测得 $\angle ABC = 150^{\circ}$,$BC = 1600m$,$\angle BCD = 105^{\circ}$,求 $B$、$D$ 两点的距离。


答案:
解:过点C作CE⊥AD
因为∠ABC=150°
所以∠CBD=180°-∠ABC=30°
所以∠BCE=90°-30°=60°
因为∠BCD=105°
所以∠DCE=∠BCD-∠BCE=45°
所以CE=DE
因为$sin∠BCE=sin{30}°=\frac {CE}{BC}=\frac {CE}{1600}=\frac {1}{2}$
所以CE=800
所以CE=DE=800
所以∠ECD=45°
所以∠BCE=60°
所以$BE=\sqrt{3}CE=800\sqrt{3}m$
所以$BD=800\sqrt{3}+800m$
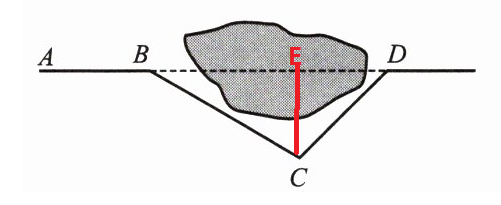
解:过点C作CE⊥AD
因为∠ABC=150°
所以∠CBD=180°-∠ABC=30°
所以∠BCE=90°-30°=60°
因为∠BCD=105°
所以∠DCE=∠BCD-∠BCE=45°
所以CE=DE
因为$sin∠BCE=sin{30}°=\frac {CE}{BC}=\frac {CE}{1600}=\frac {1}{2}$
所以CE=800
所以CE=DE=800
所以∠ECD=45°
所以∠BCE=60°
所以$BE=\sqrt{3}CE=800\sqrt{3}m$
所以$BD=800\sqrt{3}+800m$

8. 在 $\triangle ABC$ 中,$\angle A = 60^{\circ}$,$AC = 4$。若 $\triangle ABC$ 是锐角三角形,则边 $AB$ 长的取值范围是
$2 < AB < 8$
。答案:2<AB<8