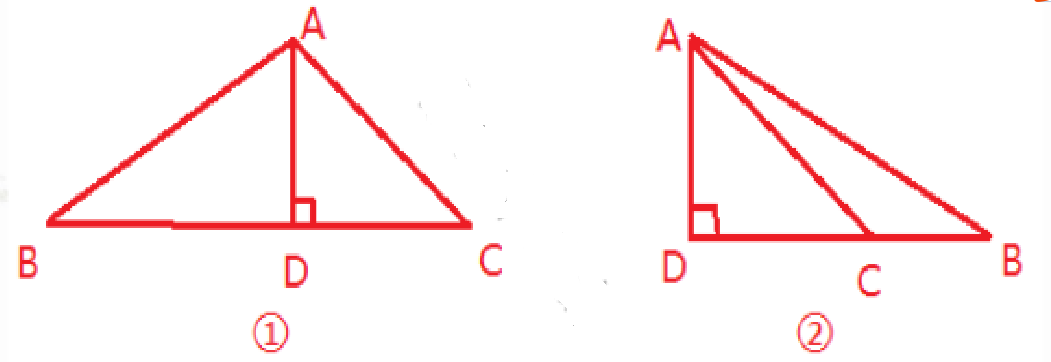例 2 人要安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角 $\alpha$ 一般要满足 $53^{\circ} \leqslant \alpha \leqslant 72^{\circ}$. 如图 7.4.1,梯子 $AB$ 斜靠在竖直的墙 $AO$ 上,$AB$ 的长为 $4 \mathrm{~m}$.
(1) 若要安全使用这架梯子,则梯子顶端 $A$ 与地面距离的最大值可为多少?
(2) 当梯子底端 $B$ 距离墙面 $1.64 \mathrm{~m}$ 时,计算 $\angle A B O$,并判断此时人是否能安全使用这架梯子. (参考数据:$\sin 53^{\circ} \approx 0.80$,$\cos 53^{\circ} \approx 0.60$,$\sin 72^{\circ} \approx 0.95$,$\cos 72^{\circ} \approx 0.31$,$\sin 66^{\circ} \approx 0.91$,$\cos 66^{\circ} \approx 0.41$)

(1) 若要安全使用这架梯子,则梯子顶端 $A$ 与地面距离的最大值可为多少?
(2) 当梯子底端 $B$ 距离墙面 $1.64 \mathrm{~m}$ 时,计算 $\angle A B O$,并判断此时人是否能安全使用这架梯子. (参考数据:$\sin 53^{\circ} \approx 0.80$,$\cos 53^{\circ} \approx 0.60$,$\sin 72^{\circ} \approx 0.95$,$\cos 72^{\circ} \approx 0.31$,$\sin 66^{\circ} \approx 0.91$,$\cos 66^{\circ} \approx 0.41$)

答案:解:(1)由题意可得:当a=72°时,AO取得最大值
在Rt△AOB中,$sin∠ABO=\frac {AO}{AB}$
所以$AO=AB×sin∠ABO=4×sin{72}°=3.8(\mathrm {m})$
所以梯子顶端A与地面距离的最大值为3.8m
(2)在Rt△AOB中,$cos∠ABO=\frac {BO}{AB}=\frac {1.64}{4}=0.41$
所以∠ABO≈66°
因为53°<66°<72°
所以人能安全使用这架梯子
在Rt△AOB中,$sin∠ABO=\frac {AO}{AB}$
所以$AO=AB×sin∠ABO=4×sin{72}°=3.8(\mathrm {m})$
所以梯子顶端A与地面距离的最大值为3.8m
(2)在Rt△AOB中,$cos∠ABO=\frac {BO}{AB}=\frac {1.64}{4}=0.41$
所以∠ABO≈66°
因为53°<66°<72°
所以人能安全使用这架梯子
1. 在 $\mathrm{Rt} \triangle A B C$ 中,$\angle C=90^{\circ}$,$B C=\sqrt{5}$,$A C=\sqrt{15}$,则 $\angle A$ 的度数为
$30^{\circ}$
.答案:30°
2. 在 $\triangle A B C$ 中,$\angle A$、$\angle B$ 都是锐角,$\sin A=\frac{\sqrt{3}}{2}$,$\tan B=\sqrt{3}$,则 $\triangle A B C$ 的形状是
等边三角形
.答案:等边三角形
3. 在 $\mathrm{Rt} \triangle A B C$ 中,若 $\cos A=\frac{1}{2}$,则 $\sin A=$
$\frac{\sqrt{3}}{2}$
.答案:$3. \frac{\sqrt{3}}{2}.$
解析:
在$\mathrm{Rt}\triangle ABC$中,$\cos A = \frac{1}{2}$,且$0° < A < 90°$,则$\angle A = 60°$,所以$\sin A = \sin 60° = \frac{\sqrt{3}}{2}$。
$\frac{\sqrt{3}}{2}$
$\frac{\sqrt{3}}{2}$
二、解答题
4. 求满足下列各式的锐角 $\alpha$:
(1) $2 \sin \left(\alpha-20^{\circ}\right)=1$;
(2) $\tan ^{2} \alpha+\tan \alpha-2=0$.
4. 求满足下列各式的锐角 $\alpha$:
(1) $2 \sin \left(\alpha-20^{\circ}\right)=1$;
(2) $\tan ^{2} \alpha+\tan \alpha-2=0$.
答案:解:$ (1)sin(a- 20°)=\frac {1}{2}$
a-20°=30°
a=50°
解:(2) (tana + 2)(tana- 1)= 0
tana+ 2= 0或tana- 1 = 0
tana= - 2或tana= 1
因为$tana\gt 0$
tana= 1
a=45°
a-20°=30°
a=50°
解:(2) (tana + 2)(tana- 1)= 0
tana+ 2= 0或tana- 1 = 0
tana= - 2或tana= 1
因为$tana\gt 0$
tana= 1
a=45°
5. 已知在 $\triangle A B C$ 中,$A D$ 是边 $B C$ 上的高,$A D=2$,$A C=2 \sqrt{2}$,$A B=4$,求 $\angle B A C$ 的度数.
答案:
解:如图①,$sinB=\frac {AD}{AB}=\frac {1}{2},$∠B=30°
$sinC=\frac {AD}{AC}=\frac {\sqrt{2}}{2},$∠C= 45°
所以∠BAC=180°-30°-45°=105°
如图②,$cos∠DAC =\frac {AD}{AC}=\frac {\sqrt{2}}{2},$∠DAC= 45°
$cos∠DAB=\frac {AD}{AB}=\frac {1}{2},$∠DAB=60°
所以∠BAC = 60°-45° = 15°
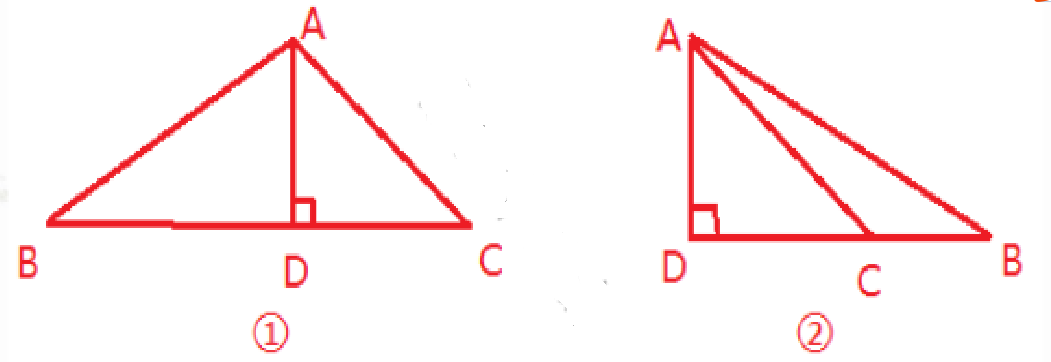
解:如图①,$sinB=\frac {AD}{AB}=\frac {1}{2},$∠B=30°
$sinC=\frac {AD}{AC}=\frac {\sqrt{2}}{2},$∠C= 45°
所以∠BAC=180°-30°-45°=105°
如图②,$cos∠DAC =\frac {AD}{AC}=\frac {\sqrt{2}}{2},$∠DAC= 45°
$cos∠DAB=\frac {AD}{AB}=\frac {1}{2},$∠DAB=60°
所以∠BAC = 60°-45° = 15°