6. 如图,某一时刻太阳光从窗户射人房间内,窗户的高度 $A F=2 \mathrm{~m}$,窗台的高度 $C F=1 \mathrm{~m}$,窗外水平遮阳篷的宽度 $A D=0.8 \mathrm{~m}$,房间内被太阳光照射的区域的宽度 $E P=(2 \sqrt{3}-0.8) \mathrm{m}$,求太阳光与地面的夹角 $\angle D P C$ 的度数.
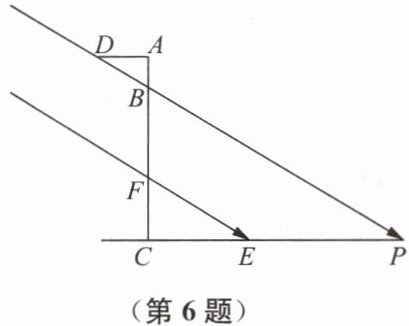

答案:解:由图形可得:AD//CP
设∠DPC的度数为a
所以∠ADB=∠CEF=∠DPC=a
因为CF=1
所以$\frac {1}{CE}=tanα$
所以$CE=\frac {1}{tanα}$
因为$\frac {BC}{CP}=tanα$
所以$BC=tanα×CP=tanα(\frac {1}{tanα}+2\sqrt{3}-0.8)=1+(2\sqrt{3}-0.8)tanα$
因为$\frac {AB}{AD}=tanα$
所以AB=0.8tanα
因为AC=AF+CF=3m
所以$1+(2\sqrt{3}-0.8)tanα+0.8tanα=3$
所以$tanα=\frac {\sqrt{3}}{3}$
所以α=30°.
设∠DPC的度数为a
所以∠ADB=∠CEF=∠DPC=a
因为CF=1
所以$\frac {1}{CE}=tanα$
所以$CE=\frac {1}{tanα}$
因为$\frac {BC}{CP}=tanα$
所以$BC=tanα×CP=tanα(\frac {1}{tanα}+2\sqrt{3}-0.8)=1+(2\sqrt{3}-0.8)tanα$
因为$\frac {AB}{AD}=tanα$
所以AB=0.8tanα
因为AC=AF+CF=3m
所以$1+(2\sqrt{3}-0.8)tanα+0.8tanα=3$
所以$tanα=\frac {\sqrt{3}}{3}$
所以α=30°.
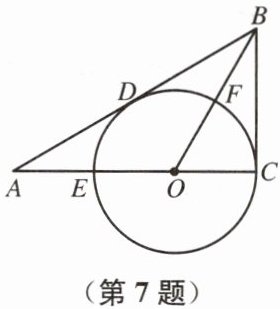
7. 如图,在 $\mathrm{Rt} \triangle A B C$ 中,$\angle A C B=90^{\circ}$,点 $O$ 在 $A C$ 上,以 $O C$ 为半径的圆交 $A B$ 于点 $D$,交 $A C$ 于点 $E$. 连接 $O B$ 交 $\odot O$ 于点 $F$,且 $B D=B C$.
(1) 求证:$A B$ 是 $\odot O$ 的切线.
(2) 若 $A D=\sqrt{3}$,$A E=1$,求 $\overgroup{C F}$ 的长.
(1) 求证:$A B$ 是 $\odot O$ 的切线.
(2) 若 $A D=\sqrt{3}$,$A E=1$,求 $\overgroup{C F}$ 的长.

答案:(1) 证明:连接 $OD$。
因为 $OC = OD$,$BD = BC$,$OB = OB$,
所以 $\triangle OBD \cong \triangle OBC$(SSS)。
所以 $\angle ODB = \angle OCB$。
因为 $\angle ACB = 90°$,所以 $\angle ODB = 90°$。
因为 $OD$ 是 $\odot O$ 的半径,所以 $AB$ 是 $\odot O$ 的切线。
(2) 设 $\odot O$ 的半径为 $r$,则 $OE = OD = OC = r$。
因为 $AE = 1$,所以 $AO = AE + OE = 1 + r$,$AC = AE + EC = 1 + 2r$。
在 $\mathrm{Rt}\triangle ADO$ 中,$AD = \sqrt{3}$,由勾股定理得:
$AD^2 + OD^2 = AO^2$,即 $(\sqrt{3})^2 + r^2 = (1 + r)^2$。
解得 $r = 1$,所以 $AO = 2$,$OD = 1$。
在 $\mathrm{Rt}\triangle ADO$ 中,$\sin \angle AOD = \frac{AD}{AO} = \frac{\sqrt{3}}{2}$,所以 $\angle AOD = 60°$。
所以 $\angle COD = 180° - \angle AOD = 120°$。
因为 $\triangle OBD \cong \triangle OBC$,所以 $\angle BOC = \angle BOF$。
设 $\angle BOC = \angle BOF = x$,则 $\angle COD = \angle COF + \angle FOD = 2x = 120°$,解得 $x = 60°$。
所以 $\angle COF = 60°$,$\overset{\frown}{CF}$ 的长为 $\frac{60\pi × 1}{180} = \frac{\pi}{3}$。
答案:(2) $\frac{\pi}{3}$
因为 $OC = OD$,$BD = BC$,$OB = OB$,
所以 $\triangle OBD \cong \triangle OBC$(SSS)。
所以 $\angle ODB = \angle OCB$。
因为 $\angle ACB = 90°$,所以 $\angle ODB = 90°$。
因为 $OD$ 是 $\odot O$ 的半径,所以 $AB$ 是 $\odot O$ 的切线。
(2) 设 $\odot O$ 的半径为 $r$,则 $OE = OD = OC = r$。
因为 $AE = 1$,所以 $AO = AE + OE = 1 + r$,$AC = AE + EC = 1 + 2r$。
在 $\mathrm{Rt}\triangle ADO$ 中,$AD = \sqrt{3}$,由勾股定理得:
$AD^2 + OD^2 = AO^2$,即 $(\sqrt{3})^2 + r^2 = (1 + r)^2$。
解得 $r = 1$,所以 $AO = 2$,$OD = 1$。
在 $\mathrm{Rt}\triangle ADO$ 中,$\sin \angle AOD = \frac{AD}{AO} = \frac{\sqrt{3}}{2}$,所以 $\angle AOD = 60°$。
所以 $\angle COD = 180° - \angle AOD = 120°$。
因为 $\triangle OBD \cong \triangle OBC$,所以 $\angle BOC = \angle BOF$。
设 $\angle BOC = \angle BOF = x$,则 $\angle COD = \angle COF + \angle FOD = 2x = 120°$,解得 $x = 60°$。
所以 $\angle COF = 60°$,$\overset{\frown}{CF}$ 的长为 $\frac{60\pi × 1}{180} = \frac{\pi}{3}$。
答案:(2) $\frac{\pi}{3}$