例1 在Rt△ABC中,∠C=90°,请根据下列条件解直角三角形.
(1)a=10,∠A=45°;
(2)a=5,b=5√3.
(1)a=10,∠A=45°;
(2)a=5,b=5√3.
答案:解: (1)在Rt△ABC中
因为∠A=45°,∠C=90°
所以∠B=45°
因为a=10,∠A=∠B
所以b=a= 10,$ c=\sqrt{a²+b²}=10\sqrt{2}$
(2)在Rt△ABC中,
因为a=5,$ b= 5\sqrt{3}$
所以$c=\sqrt{a²+b²}= 10$
因为$sinA=\frac {a}{c}=\frac {1}{2}$
所以∠A=30°,∠B= 60°
因为∠A=45°,∠C=90°
所以∠B=45°
因为a=10,∠A=∠B
所以b=a= 10,$ c=\sqrt{a²+b²}=10\sqrt{2}$
(2)在Rt△ABC中,
因为a=5,$ b= 5\sqrt{3}$
所以$c=\sqrt{a²+b²}= 10$
因为$sinA=\frac {a}{c}=\frac {1}{2}$
所以∠A=30°,∠B= 60°
例2 如图7.5.1,已知sinα=24/25,tanβ=3,BE=20,求AB的长.


答案:
解:如图,过点A作AF⊥CD于点F,
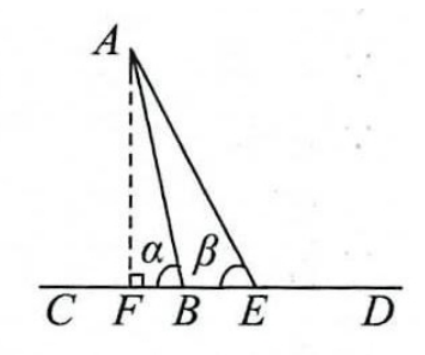
所以∠AFB= 90°.
在Rt△ABF 中,$sin a=\frac {AF}{AB}=\frac {24}{25}$
所以设AF=24x,AB=25x,
所以由勾股定理得$BF=\sqrt{AB²-AF²}=\sqrt{(25x)²-(24x)²}=7x.$
在Rt△AFE中,$tan β=\frac {AF}{EF}=3.$
因为BE=20米,
所以$\frac {24x}{7x+20}=3$
解得x=20,
所以 AB= 25x= 500.
解:如图,过点A作AF⊥CD于点F,

所以∠AFB= 90°.
在Rt△ABF 中,$sin a=\frac {AF}{AB}=\frac {24}{25}$
所以设AF=24x,AB=25x,
所以由勾股定理得$BF=\sqrt{AB²-AF²}=\sqrt{(25x)²-(24x)²}=7x.$
在Rt△AFE中,$tan β=\frac {AF}{EF}=3.$
因为BE=20米,
所以$\frac {24x}{7x+20}=3$
解得x=20,
所以 AB= 25x= 500.
1. 在Rt△ABC中,∠C=90°,∠A=45°,c=6,则a等于 (
A.3
B.2√3
C.3√2
D.6√2
C
)A.3
B.2√3
C.3√2
D.6√2
答案:C
2. 在△ABC中,AC=6,BC=10,AB=14,则∠C的度数为 (
A.100°
B.105°
C.120°
D.135°
C
)A.100°
B.105°
C.120°
D.135°
答案:2.C.
解析:
在△ABC中,已知AC=6,BC=10,AB=14,要求∠C的度数。
根据余弦定理:对于任意三角形,有$c^2 = a^2 + b^2 - 2ab\cos C$,其中$a$、$b$为角$C$的两边,$c$为角$C$的对边。
在此题中,$a = BC = 10$,$b = AC = 6$,$c = AB = 14$。
将数值代入余弦定理公式可得:
$\begin{aligned}AB^2&=AC^2 + BC^2 - 2× AC× BC×\cos C\\14^2&=6^2 + 10^2 - 2×6×10×\cos C\\196&=36 + 100 - 120×\cos C\\196&=136 - 120\cos C\\196 - 136&=-120\cos C\\60&=-120\cos C\\\cos C&=-\frac{60}{120}=-\frac{1}{2}\end{aligned}$
因为$0^{\circ} < C < 180^{\circ}$,且$\cos C = -\frac{1}{2}$,所以$C = 120^{\circ}$。
答案:C
根据余弦定理:对于任意三角形,有$c^2 = a^2 + b^2 - 2ab\cos C$,其中$a$、$b$为角$C$的两边,$c$为角$C$的对边。
在此题中,$a = BC = 10$,$b = AC = 6$,$c = AB = 14$。
将数值代入余弦定理公式可得:
$\begin{aligned}AB^2&=AC^2 + BC^2 - 2× AC× BC×\cos C\\14^2&=6^2 + 10^2 - 2×6×10×\cos C\\196&=36 + 100 - 120×\cos C\\196&=136 - 120\cos C\\196 - 136&=-120\cos C\\60&=-120\cos C\\\cos C&=-\frac{60}{120}=-\frac{1}{2}\end{aligned}$
因为$0^{\circ} < C < 180^{\circ}$,且$\cos C = -\frac{1}{2}$,所以$C = 120^{\circ}$。
答案:C
3. 在Rt△ABC中,∠C=90°,AB=4,tanA=1,则BC的长为
$2\sqrt{2}$
.答案:$2\sqrt{2}$
4. 如图,由8个全等的菱形组成的网格中,每个小菱形的边长均为2,∠ABD=120°,其中点A、B、C都在格点上,则tan∠BCD的值为

$2\sqrt{3}$
.
答案:$2\sqrt{3}$