三、解答题
5. 在△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,根据下列条件解直角三角形:
(1)b=17,c=17√2;
(2)c=20,∠A=60°.
5. 在△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,根据下列条件解直角三角形:
(1)b=17,c=17√2;
(2)c=20,∠A=60°.
答案: 解:在Rt△ABC中
因为∠C= 90°, b= 17,$c= 17\sqrt{2}$
所以$a=\sqrt{c²-b²}=17$
因为$sinA=\frac {a}{c}=\frac {17}{17\sqrt{2}}=\frac {\sqrt{2}}{2}$
所以∠A=45°,∠B=45°
解:因为∠C=90°,∠A=60°
所以∠B=30°
因为c=20
所以$a=c×sin{60}° = 10\sqrt{3},$
b= c×cos{60}°= 10
因为∠C= 90°, b= 17,$c= 17\sqrt{2}$
所以$a=\sqrt{c²-b²}=17$
因为$sinA=\frac {a}{c}=\frac {17}{17\sqrt{2}}=\frac {\sqrt{2}}{2}$
所以∠A=45°,∠B=45°
解:因为∠C=90°,∠A=60°
所以∠B=30°
因为c=20
所以$a=c×sin{60}° = 10\sqrt{3},$
b= c×cos{60}°= 10
6. 如图,在△ABC中,AD⊥BC,垂足为D,AE是边BC上的中线,AB=10,AD=6,tan∠ACB=1.
(1)求BC的长;
(2)求sin∠DAE的值.

(1)求BC的长;
(2)求sin∠DAE的值.

答案:6. (1) 14; (2) $\frac{\sqrt{37}}{37}$.
解析:
(1)在$Rt\triangle ABD$中,$AB=10$,$AD=6$,由勾股定理得$BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{10^{2}-6^{2}}=8$。
在$Rt\triangle ADC$中,$\tan\angle ACB = 1$,即$\frac{AD}{DC}=1$,所以$DC=AD=6$。
则$BC=BD + DC=8 + 6=14$。
(2)因为$AE$是$BC$边上的中线,$BC=14$,所以$BE=\frac{1}{2}BC=7$。
又因为$BD=8$,所以$DE=BD - BE=8 - 7=1$。
在$Rt\triangle ADE$中,$AD=6$,$DE=1$,由勾股定理得$AE=\sqrt{AD^{2}+DE^{2}}=\sqrt{6^{2}+1^{2}}=\sqrt{37}$。
所以$\sin\angle DAE=\frac{DE}{AE}=\frac{1}{\sqrt{37}}=\frac{\sqrt{37}}{37}$。
在$Rt\triangle ADC$中,$\tan\angle ACB = 1$,即$\frac{AD}{DC}=1$,所以$DC=AD=6$。
则$BC=BD + DC=8 + 6=14$。
(2)因为$AE$是$BC$边上的中线,$BC=14$,所以$BE=\frac{1}{2}BC=7$。
又因为$BD=8$,所以$DE=BD - BE=8 - 7=1$。
在$Rt\triangle ADE$中,$AD=6$,$DE=1$,由勾股定理得$AE=\sqrt{AD^{2}+DE^{2}}=\sqrt{6^{2}+1^{2}}=\sqrt{37}$。
所以$\sin\angle DAE=\frac{DE}{AE}=\frac{1}{\sqrt{37}}=\frac{\sqrt{37}}{37}$。
7. 如图,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c.
(1)证明S△ABC=1/2absinC=1/2acsinB=1/2bcsinA;
(2)若在△ABC中,∠B=60°,∠C=45°,c=2,求sinA的值.

(1)证明S△ABC=1/2absinC=1/2acsinB=1/2bcsinA;
(2)若在△ABC中,∠B=60°,∠C=45°,c=2,求sinA的值.

答案:
解:(1)证明:过点A作AD⊥BC,垂足为点D,如图所示,
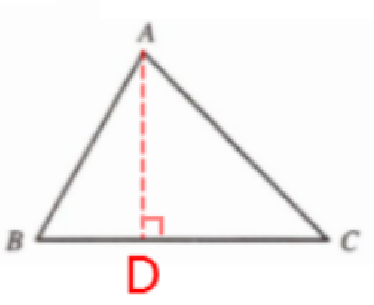
在Rt△ACD中,
因为$sinC = \frac {AD}{b}$
所以AD= bsinC
$S_{△ABC}= \frac {1}{2}a×AD=\frac {1}{2}absinC$
同理可得,$ S_{△ABC}= \frac {1}{2}acsinB=\frac {1}{2}bcsinA$
$S_{△ABC}= \frac {1}{2}absinC =\frac {1}{2}acsinB=\frac {1}{2}bcsinA$
(2)在Rt△ABD中,
因为c=2 ,∠B=60°
所以$AD=c×sin_{60}°=\sqrt{3},$$BD= c.cos_{60}°= 1$
在Rt△ACD中,
因为$AD=\sqrt{3},$∠C= 45°
所以$CD= AD=\sqrt{3},$$b=\frac {AD}{sin_{45}°}=\sqrt{6}$
所以$a= BD+ CD=1+\sqrt{3}$
$S_{△ABC}=\frac {1}{2}a×AD=\frac {3+\sqrt{3}}{2}$
因为$S_{△ABC}=\frac {1}{2}bcsinA$
所以$sinA=\frac {2S_{△ABC}}{bc}=\frac {\sqrt{2}+\sqrt{6}}{4}$
解:(1)证明:过点A作AD⊥BC,垂足为点D,如图所示,

在Rt△ACD中,
因为$sinC = \frac {AD}{b}$
所以AD= bsinC
$S_{△ABC}= \frac {1}{2}a×AD=\frac {1}{2}absinC$
同理可得,$ S_{△ABC}= \frac {1}{2}acsinB=\frac {1}{2}bcsinA$
$S_{△ABC}= \frac {1}{2}absinC =\frac {1}{2}acsinB=\frac {1}{2}bcsinA$
(2)在Rt△ABD中,
因为c=2 ,∠B=60°
所以$AD=c×sin_{60}°=\sqrt{3},$$BD= c.cos_{60}°= 1$
在Rt△ACD中,
因为$AD=\sqrt{3},$∠C= 45°
所以$CD= AD=\sqrt{3},$$b=\frac {AD}{sin_{45}°}=\sqrt{6}$
所以$a= BD+ CD=1+\sqrt{3}$
$S_{△ABC}=\frac {1}{2}a×AD=\frac {3+\sqrt{3}}{2}$
因为$S_{△ABC}=\frac {1}{2}bcsinA$
所以$sinA=\frac {2S_{△ABC}}{bc}=\frac {\sqrt{2}+\sqrt{6}}{4}$
8. 规定:有两个内角的差为90°的三角形称为“反直角三角形”.如图,在△ABC中,AB=AC=5,BC=8,P为边BC上一点,若△APC为“反直角三角形”,求BP的长.


答案:8. $\frac{25}{4}$或$\frac{11}{2}$.
解析:
解:过点$A$作$AD⊥ BC$于点$D$,
$\because AB=AC=5$,$BC=8$,
$\therefore BD=DC=4$,$AD=\sqrt{AC^{2}-DC^{2}}=\sqrt{5^{2}-4^{2}}=3$。
设$BP=x$,则$PC=8 - x$,$PD=|4 - x|$。
情况1:$\angle PAC - \angle C = 90°$
过点$P$作$PE⊥ AC$于点$E$,
$\because \angle PAC = 90° + \angle C$,
$\therefore \angle PAE = 90° - \angle C$,
$\therefore \triangle AEP \sim \triangle CDA$,
$\frac{AE}{CD} = \frac{EP}{AD} = \frac{AP}{AC}$,
$AP^{2} = AD^{2} + PD^{2} = 3^{2} + (4 - x)^{2} = x^{2} - 8x + 25$,
$\frac{AP}{AC} = \frac{\sqrt{x^{2} - 8x + 25}}{5}$,
$AE = \frac{4\sqrt{x^{2} - 8x + 25}}{5}$,$EP = \frac{3\sqrt{x^{2} - 8x + 25}}{5}$,
$CE = AC - AE = 5 - \frac{4\sqrt{x^{2} - 8x + 25}}{5}$,
由$EP^{2} + CE^{2} = PC^{2}$,得:
$\left(\frac{3\sqrt{x^{2} - 8x + 25}}{5}\right)^{2} + \left(5 - \frac{4\sqrt{x^{2} - 8x + 25}}{5}\right)^{2} = (8 - x)^{2}$,
化简得$x = \frac{25}{4}$。
情况2:$\angle C - \angle PAC = 90°$
过点$P$作$PF⊥ AC$延长线于点$F$,
$\angle PCF = 90° - \angle PAC$,
$\triangle PFC \sim \triangle ADC$,
$\frac{CF}{CD} = \frac{PF}{AD} = \frac{PC}{AC}$,
$CF = \frac{4(8 - x)}{5}$,$PF = \frac{3(8 - x)}{5}$,
$AF = AC + CF = 5 + \frac{4(8 - x)}{5}$,
由$AF^{2} + PF^{2} = AP^{2}$,得:
$\left(5 + \frac{4(8 - x)}{5}\right)^{2} + \left(\frac{3(8 - x)}{5}\right)^{2} = x^{2} - 8x + 25$,
化简得$x = \frac{11}{2}$。
综上,$BP$的长为$\frac{25}{4}$或$\frac{11}{2}$。
$\boxed{\frac{25}{4}或\frac{11}{2}}$
$\because AB=AC=5$,$BC=8$,
$\therefore BD=DC=4$,$AD=\sqrt{AC^{2}-DC^{2}}=\sqrt{5^{2}-4^{2}}=3$。
设$BP=x$,则$PC=8 - x$,$PD=|4 - x|$。
情况1:$\angle PAC - \angle C = 90°$
过点$P$作$PE⊥ AC$于点$E$,
$\because \angle PAC = 90° + \angle C$,
$\therefore \angle PAE = 90° - \angle C$,
$\therefore \triangle AEP \sim \triangle CDA$,
$\frac{AE}{CD} = \frac{EP}{AD} = \frac{AP}{AC}$,
$AP^{2} = AD^{2} + PD^{2} = 3^{2} + (4 - x)^{2} = x^{2} - 8x + 25$,
$\frac{AP}{AC} = \frac{\sqrt{x^{2} - 8x + 25}}{5}$,
$AE = \frac{4\sqrt{x^{2} - 8x + 25}}{5}$,$EP = \frac{3\sqrt{x^{2} - 8x + 25}}{5}$,
$CE = AC - AE = 5 - \frac{4\sqrt{x^{2} - 8x + 25}}{5}$,
由$EP^{2} + CE^{2} = PC^{2}$,得:
$\left(\frac{3\sqrt{x^{2} - 8x + 25}}{5}\right)^{2} + \left(5 - \frac{4\sqrt{x^{2} - 8x + 25}}{5}\right)^{2} = (8 - x)^{2}$,
化简得$x = \frac{25}{4}$。
情况2:$\angle C - \angle PAC = 90°$
过点$P$作$PF⊥ AC$延长线于点$F$,
$\angle PCF = 90° - \angle PAC$,
$\triangle PFC \sim \triangle ADC$,
$\frac{CF}{CD} = \frac{PF}{AD} = \frac{PC}{AC}$,
$CF = \frac{4(8 - x)}{5}$,$PF = \frac{3(8 - x)}{5}$,
$AF = AC + CF = 5 + \frac{4(8 - x)}{5}$,
由$AF^{2} + PF^{2} = AP^{2}$,得:
$\left(5 + \frac{4(8 - x)}{5}\right)^{2} + \left(\frac{3(8 - x)}{5}\right)^{2} = x^{2} - 8x + 25$,
化简得$x = \frac{11}{2}$。
综上,$BP$的长为$\frac{25}{4}$或$\frac{11}{2}$。
$\boxed{\frac{25}{4}或\frac{11}{2}}$