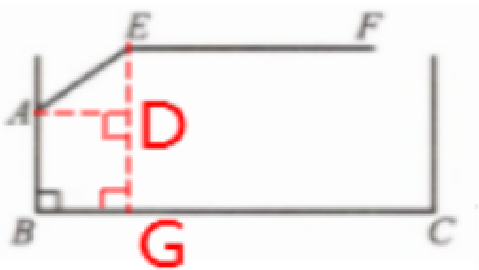
例 1 某地下车库出口处设立了“两段式栏杆”,点 $ A $ 是栏杆转动的支点,点 $ E $ 是栏杆两段的连接点. 当车辆经过时,栏杆 $ AEF $ 升起后的位置如图 7.6.1,其中 $ AB ⊥ BC $,$ EF // BC $,$ \angle EAB = 120° $,$ AB = AE = 1.6 \mathrm{ m} $. 求当车辆经过时,栏杆 $ EF $ 段距离地面的高度.


答案:
解:过点E作EG⊥BC,垂足为点G ,
过点A作AD⊥EG,垂足为点D ,如图所示
因为EG⊥BC, AD⊥EG,AB⊥BC
所以四边形ABGD为矩形
所以∠EAD= 120°-90°=30° , AB=DG=1.6m ;
在Rt△ADE中
因为AE=1.6m,∠EAD= 30°
所以$ED= AE×sin_{30}°=0.8m$
所以EG=ED+ DF=2.4m ,
即栏杆EF段距离底面的高度为2.4米。
解:过点E作EG⊥BC,垂足为点G ,
过点A作AD⊥EG,垂足为点D ,如图所示
因为EG⊥BC, AD⊥EG,AB⊥BC
所以四边形ABGD为矩形
所以∠EAD= 120°-90°=30° , AB=DG=1.6m ;
在Rt△ADE中
因为AE=1.6m,∠EAD= 30°
所以$ED= AE×sin_{30}°=0.8m$
所以EG=ED+ DF=2.4m ,
即栏杆EF段距离底面的高度为2.4米。

例 2 如图 7.6.2 是某种玻璃淋浴房的俯视示意图,$ AE $ 与 $ DE $ 是墙,$ AB $ 与 $ CD $ 是固定的玻璃隔板,$ BC $ 是门框,测得 $ AB = BC = CD = 60 \mathrm{ cm} $,$ \angle ABC = \angle BCD = 135° $,$ MN $ 是一扇推拉门,推动推拉门时,两端点 $ M $,$ N $ 分别在 $ BC $,$ CD $ 对应的轨道上滑动. 当点 $ N $ 与点 $ C $ 重合时,推拉门与门框完全闭合;当点 $ N $ 滑动到限位点 $ P $ 处时,门打开至最大,此时测得 $ \angle CNM = 6° $.
(1) 在门从闭合到打开至最大的过程中,
① $ \angle CMN $ 的最小值为
② $ \triangle CMN $ 面积的变化情况是 (
A. 越来越大
B. 越来越小
C. 先增大后减小

(2) 当 $ \angle CMN = 30° $ 时,求 $ \triangle CMN $ 的面积.
(1) 在门从闭合到打开至最大的过程中,
① $ \angle CMN $ 的最小值为
0
$ ° $,最大值为39
$ ° $;② $ \triangle CMN $ 面积的变化情况是 (
C
)A. 越来越大
B. 越来越小
C. 先增大后减小

(2) 当 $ \angle CMN = 30° $ 时,求 $ \triangle CMN $ 的面积.
答案:例$2 $解$(1)①$当点$N$与点$C$重合时,推拉门与门框完全闭合,此时$\angle CMN$有最小值,为$0^{\circ}。$当点$N$滑动到限位点$P$处时,推拉门推至最大,此时$\angle CNM = 6^{\circ},$则此时$\angle CMN$有最大值。$\because\angle CNM = 6^{\circ},$$\angle BCD = 135^{\circ},$$\therefore\angle CMN = 180^{\circ}-6^{\circ}-135^{\circ}=39^{\circ},$即$\angle CMN$的最大值为$39^{\circ}。$故答案为$0,$$39。$$②$根据特殊情况分析如下:当点$N$与点$C$重合时,$S_{\triangle CMN}=0;$如果没有点$P$的限制,那么当点$N$与点$D$重合时,$S_{\triangle CMN}=0,$$\therefore\triangle CMN$面积的变化情况是先增大后减小,故选$C。$$(2)$如图$,$过点$N$作$NH⊥BC$交$BC$的延长线于点$H.$依题意可知$MN = BC = 60.$∵$∠CMN = 30°,$∴$NH=\frac{1}{2}MN = 30,MH = MN·\cos30°=\frac{\sqrt{3}}{2}MN = 30\sqrt{3}.$∵$∠BCD = 135°,$∴$∠NCH = ∠CNH = 45°,$∴$CH = NH = 30,$∴$MC = 30\sqrt{3}-30,$∴$S_{△CMN}=\frac{1}{2}×(30\sqrt{3}-30)×30=(450\sqrt{3}-450)cm^{2}.$答$:$当$∠CMN = 30°$时$,△CMN$的面积为$(450\sqrt{3}-450)cm^{2}$