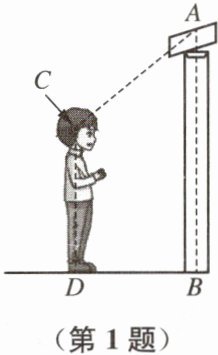
1. 某公司在门禁上方安装了摄像头,如图,已知摄像头与地面的距离 $ AB = 2.7 \mathrm{ m} $,某人目高 $ CD = 1.8 \mathrm{ m} $,摄像头的张角 $ \angle A = 53° $. 求该人与摄像头的水平距离. (精确到 $ 0.1 \mathrm{ m} $,参考数据:$ \sin 53° \approx 0.8 $,$ \cos 53° \approx 0.6 $,$ \tan 53° \approx 1.33 $)

答案:1. 1.2 m.
解析:
解:过点C作CE⊥AB于点E,
则四边形CDBE为矩形,
∴CE=BD,BE=CD=1.8m,
∴AE=AB-BE=2.7-1.8=0.9m,
在Rt△ACE中,∠A=53°,
tan∠A= $\frac{CE}{AE}$,
∴CE=AE·tan53°≈0.9×1.33≈1.2m,
即该人与摄像头的水平距离BD=CE≈1.2m.
答:该人与摄像头的水平距离约为1.2m.
则四边形CDBE为矩形,
∴CE=BD,BE=CD=1.8m,
∴AE=AB-BE=2.7-1.8=0.9m,
在Rt△ACE中,∠A=53°,
tan∠A= $\frac{CE}{AE}$,
∴CE=AE·tan53°≈0.9×1.33≈1.2m,
即该人与摄像头的水平距离BD=CE≈1.2m.
答:该人与摄像头的水平距离约为1.2m.
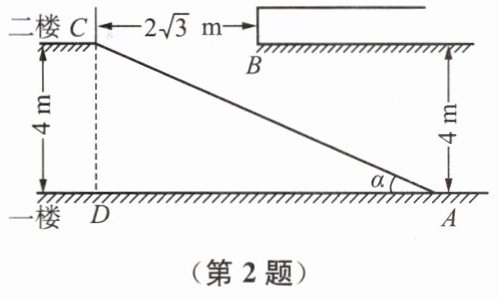
2. 某大型超市为方便顾客购物,准备在一楼至二楼之间安装自动扶梯(如图),楼顶与地面平行. 要使身高 $ 2 \mathrm{ m} $ 以下的人在笔直站立的情况下搭乘自动扶梯时,在 $ B $ 处不碰到头部. 请你计算:自动扶梯与一楼地面的夹角 $ \alpha $ 最小为多少度.

答案:
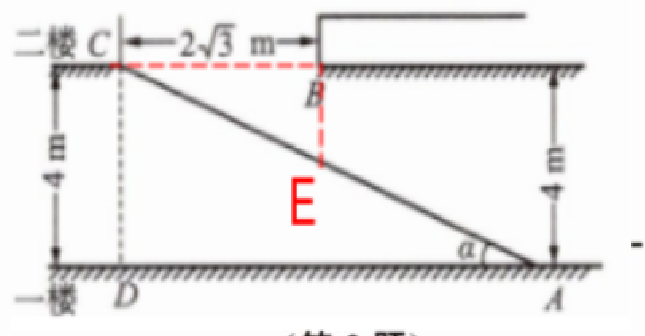
解:连接BC ,作BE⊥BC,BE与AC交于点E
由题意得,
BC//AD ,$ BC=2\sqrt{3}m,$BE=2m
在Rt△CBE中,
因为$BC=2\sqrt{3}m,$BE=2m
所以$tan∠BCE =\frac {BE}{BC}=\frac {2}{2\sqrt{3}}=\frac {\sqrt{3}}{3}$
所以∠BCE= 30°
因为BC//AD
所以α=∠BCE=30°
答:自动扶梯与一楼底面的夹角a最小为30°
解:连接BC ,作BE⊥BC,BE与AC交于点E
由题意得,
BC//AD ,$ BC=2\sqrt{3}m,$BE=2m
在Rt△CBE中,
因为$BC=2\sqrt{3}m,$BE=2m
所以$tan∠BCE =\frac {BE}{BC}=\frac {2}{2\sqrt{3}}=\frac {\sqrt{3}}{3}$
所以∠BCE= 30°
因为BC//AD
所以α=∠BCE=30°
答:自动扶梯与一楼底面的夹角a最小为30°

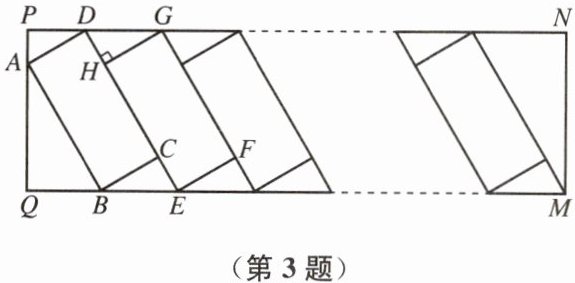
3. 为满足新能源汽车的充电需求,某小区增设了充电站. 如图是矩形 $ PQMN $ 充电站的平面示意图,充电站有若干个矩形停车位,所有停车位大小相同且并列排放,图中的矩形 $ ABCD $ 是其中一个停车位. 经测量,$ \angle ABQ = 60° $,$ AB = 5.4 \mathrm{ m} $,$ CE = 1.6 \mathrm{ m} $,$ GH ⊥ CD $.
(1) 求 $ PQ $ 的长;
(2) 该充电站有 $ 20 $ 个停车位,求 $ PN $ 的长.
(1) 求 $ PQ $ 的长;
(2) 该充电站有 $ 20 $ 个停车位,求 $ PN $ 的长.

答案:解:(1)
∵四边形PQMN是矩形,
∴∠Q=∠P=90°,
∵在Rt△ABQ中$,∠ABQ=60°,AB=5.4\mathrm {m},$
∴$AQ=AB·sin∠ABQ=\frac{27\sqrt{3}}{10}(\mathrm {m}),∠QAB=30°.$
∵四边形ABCD是矩形,
∴AD=BC,∠BAD=∠BCD=∠ABC=∠BCE=90°,
∴∠CBE=30°,
∴$BC=\frac{CE}{tan∠CBE}=\frac{8\sqrt{3}}{5}(\mathrm {m}),$
∴$AD=\frac{8\sqrt{3}}{5}\ \mathrm {m}.$
∵∠PAD=180°-30°-90°=60°,
∴$AP=AD×cos∠PAD=\frac{4\sqrt{3}}{5}(\mathrm {m}),$
∴$PQ=AP+AQ=\frac{7\sqrt{3}}{2}(\mathrm {m})$
∴PQ的长为$\frac{7\sqrt{3}}{2}\mathrm {m}$
∵四边形PQMN是矩形,
∴∠Q=∠P=90°,
∵在Rt△ABQ中$,∠ABQ=60°,AB=5.4\mathrm {m},$
∴$AQ=AB·sin∠ABQ=\frac{27\sqrt{3}}{10}(\mathrm {m}),∠QAB=30°.$
∵四边形ABCD是矩形,
∴AD=BC,∠BAD=∠BCD=∠ABC=∠BCE=90°,
∴∠CBE=30°,
∴$BC=\frac{CE}{tan∠CBE}=\frac{8\sqrt{3}}{5}(\mathrm {m}),$
∴$AD=\frac{8\sqrt{3}}{5}\ \mathrm {m}.$
∵∠PAD=180°-30°-90°=60°,
∴$AP=AD×cos∠PAD=\frac{4\sqrt{3}}{5}(\mathrm {m}),$
∴$PQ=AP+AQ=\frac{7\sqrt{3}}{2}(\mathrm {m})$
∴PQ的长为$\frac{7\sqrt{3}}{2}\mathrm {m}$
解:(2)在Rt△BCE中,BE=\frac{CE}{sin∠CBE}=3.2(m),
在Rt∠ABQ中,BQ=AB.cos∠ABQ=2.7(m),
∵该充电站有20个停车位,
∴QM=QB+20BE=66.7(m).
∵四边形PQMN是矩形,
∴PN=QM=66.7m
∴PN的长为66.7m