4. 如图①,在水平地面上,一辆小车通过一根绕过定滑轮的绳子将物体竖直向上提起. 起始位置如图②,此时测得点 $ A $ 到 $ BC $ 所在直线的距离 $ AC = 3 \mathrm{ m} $,$ \angle CAB = 60° $;停止位置如图③,此时测得 $ \angle CDB = 30° $,点 $ C $、$ A $、$ D $ 在同一条直线上.
(1) 求 $ AB $ 的长;
(2) 求物体上升的高度 $ CE $.

(1) 求 $ AB $ 的长;
(2) 求物体上升的高度 $ CE $.

答案:解:(1)在Rt△ABC中,AC=3m,∠CAB=60°
∴∠ABC=30°,
∴AB=2AC=6m,则AB的长为6m
(2)在Rt△ABC中,AB=6m,AC=3m
根据勾股定理得$BC= \sqrt{AB²-AC²}=3\sqrt{3}m$
在Rt△BCD中$,∠CDB=30°,sin{30}°=\frac{1}{2}$
∴$sin∠CDB=\frac{BC}{BD},$即$\frac{3\sqrt{3}}{BD}=\frac{1}{2},$
∴$BD=6\sqrt{3}m$
∴$CE=BD-BA=(6\sqrt{3}-6)m$
则物体上升的高度CE为$(6\sqrt{3}-6)m$
∴∠ABC=30°,
∴AB=2AC=6m,则AB的长为6m
(2)在Rt△ABC中,AB=6m,AC=3m
根据勾股定理得$BC= \sqrt{AB²-AC²}=3\sqrt{3}m$
在Rt△BCD中$,∠CDB=30°,sin{30}°=\frac{1}{2}$
∴$sin∠CDB=\frac{BC}{BD},$即$\frac{3\sqrt{3}}{BD}=\frac{1}{2},$
∴$BD=6\sqrt{3}m$
∴$CE=BD-BA=(6\sqrt{3}-6)m$
则物体上升的高度CE为$(6\sqrt{3}-6)m$
5. 四边形具有不稳定性,工程上可利用这一性质解决问题. 如图是某篮球架的侧面示意图,$ BE $、$ CD $、$ GF $ 为长度固定的支架,支架在点 $ A $、$ D $、$ G $ 处与立柱 $ AH $ 连接($ AH ⊥ MN $,垂足为 $ H $),在点 $ B $、$ C $ 处与篮板连接($ BC $ 所在直线垂直于 $ MN $),$ EF $ 是可以调节长度的伸缩臂(通过旋转点 $ F $ 处的螺栓可以改变 $ EF $ 的长度,使得支架 $ BE $ 绕点 $ A $ 旋转,从而改变四边形 $ ABCD $ 的形状,以调节篮板的高度). 已知 $ AD = BC $,$ DH = 208 \mathrm{ cm} $. 若测得 $ \angle GAE = 60° $ 时,点 $ C $ 距离地面的高度为 $ 288 \mathrm{ cm} $,则调节伸缩臂 $ EF $,将 $ \angle GAE $ 由 $ 60° $ 调节为 $ 54° $ 时,点 $ C $ 距离地面的高度升高了多少?
(参考数据:$ \sin 54° \approx 0.8 $,$ \cos 54° \approx 0.6 $)

(参考数据:$ \sin 54° \approx 0.8 $,$ \cos 54° \approx 0.6 $)

答案:
解:点C离地面的高度升高了,
当∠GAE =60°时,如图(1),
过点C作CK⊥AH,交AH所在直线于点K.
因为BC⊥MN,AH⊥MN,
所以BC//AD,
又因为AD = BC,
所以四边形ABCD是平行四边形,
所以AB//CD,
所以∠ADC=∠GAE = 60°.
因为点C离地面的高度为$288\ \mathrm {cm},$$ DH =208\ \mathrm {cm},$
所以$DK=80\ \mathrm {cm},$
所以$CD=\frac {DK}{cos_{60}°}=160\ \mathrm {cm}$
当∠GAE =54°时,如图(2),过点C作CK'⊥AH,垂足为K',
则∠CDK' =54°,
所以$DK' =CD×cos 54°≈96\ \mathrm {cm}.$
所以$96-80=16(\ \mathrm {cm}),$
所以点C离地面的高度升高约$16\ \mathrm {cm}.$
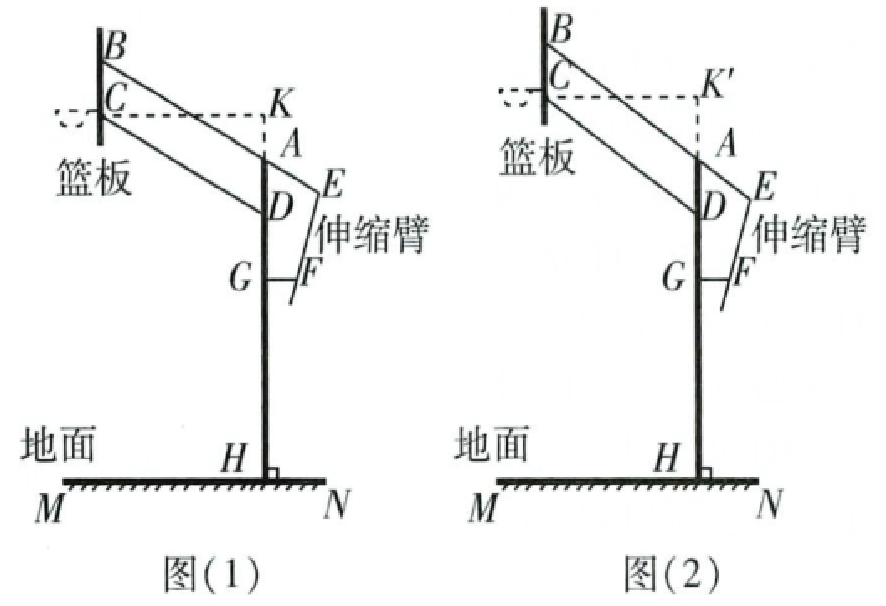
解:点C离地面的高度升高了,
当∠GAE =60°时,如图(1),
过点C作CK⊥AH,交AH所在直线于点K.
因为BC⊥MN,AH⊥MN,
所以BC//AD,
又因为AD = BC,
所以四边形ABCD是平行四边形,
所以AB//CD,
所以∠ADC=∠GAE = 60°.
因为点C离地面的高度为$288\ \mathrm {cm},$$ DH =208\ \mathrm {cm},$
所以$DK=80\ \mathrm {cm},$
所以$CD=\frac {DK}{cos_{60}°}=160\ \mathrm {cm}$
当∠GAE =54°时,如图(2),过点C作CK'⊥AH,垂足为K',
则∠CDK' =54°,
所以$DK' =CD×cos 54°≈96\ \mathrm {cm}.$
所以$96-80=16(\ \mathrm {cm}),$
所以点C离地面的高度升高约$16\ \mathrm {cm}.$
