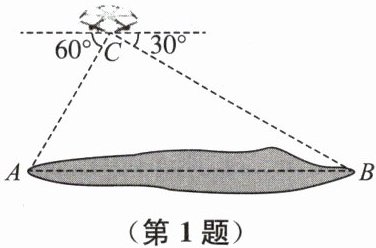
1. 如图,某科技小组用无人机测量湖泊两端 $ A $,$ B $ 的距离.他们将无人机上升至距湖面 $ 90 \mathrm{~m} $ 的点 $ C $ 处.从点 $ C $ 测得点 $ A $ 的俯角为 $ 60^{\circ} $,点 $ B $ 的俯角为 $ 30^{\circ} $($ A $,$ B $,$ C $ 三点在同一竖直平面内),则湖泊两端 $ A $,$ B $ 的距离为
$120\sqrt{3}$
$ \mathrm{m} $.
答案:1.$120\sqrt{3}$.
解析:
解:过点 $ C $ 作 $ CD ⊥ AB $ 于点 $ D $,则 $ CD = 90\ \mathrm{m} $。
在 $ \mathrm{Rt}\triangle ACD $ 中,$\angle CAD = 60°$,$\tan 60° = \frac{CD}{AD}$,即$\sqrt{3} = \frac{90}{AD}$,解得 $ AD = \frac{90}{\sqrt{3}} = 30\sqrt{3}\ \mathrm{m}$。
在 $ \mathrm{Rt}\triangle BCD $ 中,$\angle CBD = 30°$,$\tan 30° = \frac{CD}{BD}$,即$\frac{\sqrt{3}}{3} = \frac{90}{BD}$,解得 $ BD = 90\sqrt{3}\ \mathrm{m}$。
$ AB = AD + BD = 30\sqrt{3} + 90\sqrt{3} = 120\sqrt{3}\ \mathrm{m}$。
$120\sqrt{3}$
在 $ \mathrm{Rt}\triangle ACD $ 中,$\angle CAD = 60°$,$\tan 60° = \frac{CD}{AD}$,即$\sqrt{3} = \frac{90}{AD}$,解得 $ AD = \frac{90}{\sqrt{3}} = 30\sqrt{3}\ \mathrm{m}$。
在 $ \mathrm{Rt}\triangle BCD $ 中,$\angle CBD = 30°$,$\tan 30° = \frac{CD}{BD}$,即$\frac{\sqrt{3}}{3} = \frac{90}{BD}$,解得 $ BD = 90\sqrt{3}\ \mathrm{m}$。
$ AB = AD + BD = 30\sqrt{3} + 90\sqrt{3} = 120\sqrt{3}\ \mathrm{m}$。
$120\sqrt{3}$
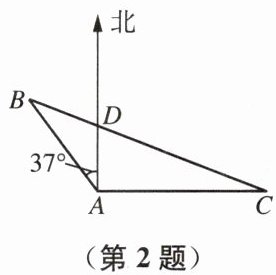
2. 如图,港口 $ B $ 位于岛 $ A $ 的北偏西 $ 37^{\circ} $ 方向,灯塔 $ C $ 在岛 $ A $ 的正东方向,$ AC = 6 \mathrm{~km} $,一艘海轮 $ D $ 在岛 $ A $ 的正北方向,且 $ B $、$ D $、$ C $ 三点在同一条直线上,$ DC = \frac{5}{2}BD $,则岛 $ A $ 与港口 $ B $ 之间的距离为
4
$ \mathrm{km} $.(参考数据:$ \sin 37^{\circ} \approx \frac{3}{5} $,$ \cos 37^{\circ} \approx \frac{4}{5} $,$ \tan 37^{\circ} \approx \frac{3}{4} $)
答案:2. 4.
解析:
设 $ BD = x \, \mathrm{km} $,则 $ DC = \frac{5}{2}x \, \mathrm{km} $,$ BC = BD + DC = \frac{7}{2}x \, \mathrm{km} $。
在 $ \mathrm{Rt}\triangle ABD $ 中,$ \angle BAD = 37° $,$ AD = AB · \cos 37° \approx AB · \frac{4}{5} $,$ BD = AB · \sin 37° \approx AB · \frac{3}{5} $,即 $ x = \frac{3}{5}AB $,故 $ AB = \frac{5}{3}x $,$ AD = \frac{4}{5}AB = \frac{4}{3}x $。
在 $ \mathrm{Rt}\triangle ADC $ 中,$ \tan \angle ACD = \frac{AD}{AC} = \frac{\frac{4}{3}x}{6} = \frac{2x}{9} $。
在 $ \mathrm{Rt}\triangle ABC $ 中,$ \tan \angle ACB = \frac{AB · \sin 37°}{AC + AB · \cos 37°} = \frac{\frac{3}{5}AB}{6 + \frac{4}{5}AB} $。
因为 $ \angle ACD = \angle ACB $,所以 $ \frac{2x}{9} = \frac{\frac{3}{5} · \frac{5}{3}x}{6 + \frac{4}{5} · \frac{5}{3}x} $,化简得 $ \frac{2x}{9} = \frac{x}{6 + \frac{4}{3}x} $。
解得 $ x = \frac{12}{5} $,则 $ AB = \frac{5}{3}x = 4 \, \mathrm{km} $。
4
在 $ \mathrm{Rt}\triangle ABD $ 中,$ \angle BAD = 37° $,$ AD = AB · \cos 37° \approx AB · \frac{4}{5} $,$ BD = AB · \sin 37° \approx AB · \frac{3}{5} $,即 $ x = \frac{3}{5}AB $,故 $ AB = \frac{5}{3}x $,$ AD = \frac{4}{5}AB = \frac{4}{3}x $。
在 $ \mathrm{Rt}\triangle ADC $ 中,$ \tan \angle ACD = \frac{AD}{AC} = \frac{\frac{4}{3}x}{6} = \frac{2x}{9} $。
在 $ \mathrm{Rt}\triangle ABC $ 中,$ \tan \angle ACB = \frac{AB · \sin 37°}{AC + AB · \cos 37°} = \frac{\frac{3}{5}AB}{6 + \frac{4}{5}AB} $。
因为 $ \angle ACD = \angle ACB $,所以 $ \frac{2x}{9} = \frac{\frac{3}{5} · \frac{5}{3}x}{6 + \frac{4}{5} · \frac{5}{3}x} $,化简得 $ \frac{2x}{9} = \frac{x}{6 + \frac{4}{3}x} $。
解得 $ x = \frac{12}{5} $,则 $ AB = \frac{5}{3}x = 4 \, \mathrm{km} $。
4
二、解答题
3. 如图,为了测量电线杆的高度 $ AB $,在离电线杆 $ 30 \mathrm{~m} $ 的 $ C $ 处,用高 $ 1.20 \mathrm{~m} $ 的测角仪 $ CD $ 测得电线杆顶端 $ B $ 的仰角 $ \alpha = 30^{\circ} $.求电线杆 $ AB $ 的高(精确到 $ 0.1 \mathrm{~m} $).
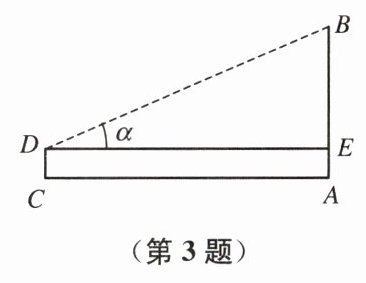
3. 如图,为了测量电线杆的高度 $ AB $,在离电线杆 $ 30 \mathrm{~m} $ 的 $ C $ 处,用高 $ 1.20 \mathrm{~m} $ 的测角仪 $ CD $ 测得电线杆顶端 $ B $ 的仰角 $ \alpha = 30^{\circ} $.求电线杆 $ AB $ 的高(精确到 $ 0.1 \mathrm{~m} $).

答案:解:由题意得, DE=AC=30m , CD=AE=1.2m ,
a=30°,∠DEB=90°
在Rt△DBE中
因为a=30°,DE= 30m
所以$BE= DE×tan_{30}° =10\sqrt{3}m$
因为AE=1.2m
所以$AB=1.2 + 10\sqrt{3}≈18.5m$
答:电线杆AB的高为18.5米。
a=30°,∠DEB=90°
在Rt△DBE中
因为a=30°,DE= 30m
所以$BE= DE×tan_{30}° =10\sqrt{3}m$
因为AE=1.2m
所以$AB=1.2 + 10\sqrt{3}≈18.5m$
答:电线杆AB的高为18.5米。
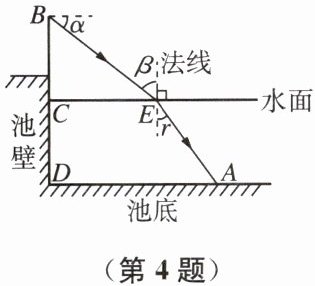
4. 科技社团用学校游泳池进行一次光的折射实验.如图,光自点 $ B $ 处发出,经水面折射到池底 $ A $ 处.已知 $ BE $ 与水平线的夹角 $ \alpha = 37^{\circ} $,点 $ B $ 到水面的距离 $ BC = 1.2 \mathrm{~m} $,点 $ A $ 处水深为 $ 1.2 \mathrm{~m} $,到池壁的距离 $ AD = 2.5 \mathrm{~m} $,点 $ B $、$ C $、$ D $ 在同一条直线上.记入射角为 $ \beta $,折射角为 $ \gamma $,求 $ \frac{\sin \beta}{\sin \gamma} $ 的值.(参考数据:$ \sin 37^{\circ} \approx 0.6 $,$ \cos 37^{\circ} \approx 0.8 $,$ \tan 37^{\circ} \approx 0.75 $)

答案:
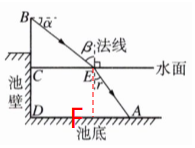
解:由题意可知,∠BEC=α=37°,∠CBE=β
∵BC=1.2m,$tan∠BEC=\frac{BC}{CE}≈0.75$
∴CE≈1.6m
∴$BE=\sqrt{BC^2+CE^2}≈\sqrt{1.2^2+1.6^2}=2m$
∴$sinβ=sin∠CBE=\frac{CE}{BE}≈\frac{1.6}{2}=0.8$
过点E作EF⊥AD于点F,则DF=CE=1.6m
∵AD=2.5m
∴AF=0.9m
∵点A处水深为1.2m,即EF=1.2m
∴$AE=\sqrt{AF^2+EF^2}=\sqrt{0.9^2+1.2^2}=1.5m$
∴$sinγ=\frac{AF}{AE}=\frac{0.9}{1.5}=0.6$
∴$\frac{sinβ}{sinγ}=\frac{0.8}{0.6}=\frac{4}{3}$

解:由题意可知,∠BEC=α=37°,∠CBE=β
∵BC=1.2m,$tan∠BEC=\frac{BC}{CE}≈0.75$
∴CE≈1.6m
∴$BE=\sqrt{BC^2+CE^2}≈\sqrt{1.2^2+1.6^2}=2m$
∴$sinβ=sin∠CBE=\frac{CE}{BE}≈\frac{1.6}{2}=0.8$
过点E作EF⊥AD于点F,则DF=CE=1.6m
∵AD=2.5m
∴AF=0.9m
∵点A处水深为1.2m,即EF=1.2m
∴$AE=\sqrt{AF^2+EF^2}=\sqrt{0.9^2+1.2^2}=1.5m$
∴$sinγ=\frac{AF}{AE}=\frac{0.9}{1.5}=0.6$
∴$\frac{sinβ}{sinγ}=\frac{0.8}{0.6}=\frac{4}{3}$