5. 如图,甲、乙两艘货轮同时从 $ A $ 港出发,分别向 $ B $、$ D $ 两港运送物资,最后到达 $ A $ 港正东方向的 $ C $ 港装运新物资.甲货轮沿 $ A $ 港的东南方向航行 $ 40 $ 海里后到达 $ B $ 港,再沿北偏东 $ 60^{\circ} $ 方向航行一定距离到达 $ C $ 港.乙货轮沿 $ A $ 港的北偏东 $ 60^{\circ} $ 方向航行一定距离到达 $ D $ 港,再沿南偏东 $ 30^{\circ} $ 方向航行一定距离到达 $ C $ 港.若甲、乙两艘货轮的速度相同(停靠 $ B $、$ D $ 两港的时间相同),哪艘货轮先到达 $ C $ 港?请通过计算说明.


答案:
解:过点B作BE⊥AC,垂足为E
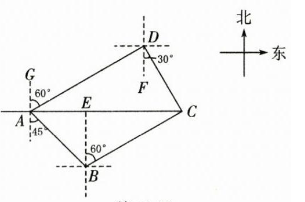
在Rt△ABE中,∠BAE=90°-45°=45°,AB=40海里
∴$AE=AB\cdot cos45°=40×\frac{\sqrt{2}}{2}=20\sqrt{2}$海里
$BE=AB\cdot sin45°=40×\frac{\sqrt{2}}{2}=20\sqrt{2}$海里
在Rt△BCE中,∠CBE=60°
∴$ CE=BE\cdot tan60°=20\sqrt{2}×\sqrt{3}=20\sqrt{6}$海里
∴$AC=AE+CE=20\sqrt{2}+20\sqrt{6}$海里
∵DF//AG
∴ ∠GAD=∠ADF=60°
∵∠CDF=30°,
∴∠ADC=∠ADF+∠CDF=90°
在Rt△ACD中,∠CAD=90°-∠GAD=30°
∴$CD=\frac{1}{2}AC=(10\sqrt{2}+10\sqrt{6}$海里,
$AD=\sqrt{3}CD=(10\sqrt{6}+30\sqrt{2})$海里
在Rt△BCE中$,∠CBE=60°,BE=20\sqrt{2}$海里
∴$BC=\frac{BE}{cos60°}=\frac{20\sqrt{2}}{\frac12}=40 \sqrt{2}$海里
∴ 甲货轮航行的路程$=AB+BC=40+40\sqrt{2}$海里
乙货轮航行的路程$=AD+CD=10\sqrt{6}+30 \sqrt{2}+10\sqrt{2}+$
$10\sqrt{6}=20 \sqrt{6}+40 \sqrt{2}$海里
∵$40+40\sqrt{2}<20\sqrt{6}+40\sqrt{2}$
∴甲货轮先到达C港
解:过点B作BE⊥AC,垂足为E

在Rt△ABE中,∠BAE=90°-45°=45°,AB=40海里
∴$AE=AB\cdot cos45°=40×\frac{\sqrt{2}}{2}=20\sqrt{2}$海里
$BE=AB\cdot sin45°=40×\frac{\sqrt{2}}{2}=20\sqrt{2}$海里
在Rt△BCE中,∠CBE=60°
∴$ CE=BE\cdot tan60°=20\sqrt{2}×\sqrt{3}=20\sqrt{6}$海里
∴$AC=AE+CE=20\sqrt{2}+20\sqrt{6}$海里
∵DF//AG
∴ ∠GAD=∠ADF=60°
∵∠CDF=30°,
∴∠ADC=∠ADF+∠CDF=90°
在Rt△ACD中,∠CAD=90°-∠GAD=30°
∴$CD=\frac{1}{2}AC=(10\sqrt{2}+10\sqrt{6}$海里,
$AD=\sqrt{3}CD=(10\sqrt{6}+30\sqrt{2})$海里
在Rt△BCE中$,∠CBE=60°,BE=20\sqrt{2}$海里
∴$BC=\frac{BE}{cos60°}=\frac{20\sqrt{2}}{\frac12}=40 \sqrt{2}$海里
∴ 甲货轮航行的路程$=AB+BC=40+40\sqrt{2}$海里
乙货轮航行的路程$=AD+CD=10\sqrt{6}+30 \sqrt{2}+10\sqrt{2}+$
$10\sqrt{6}=20 \sqrt{6}+40 \sqrt{2}$海里
∵$40+40\sqrt{2}<20\sqrt{6}+40\sqrt{2}$
∴甲货轮先到达C港
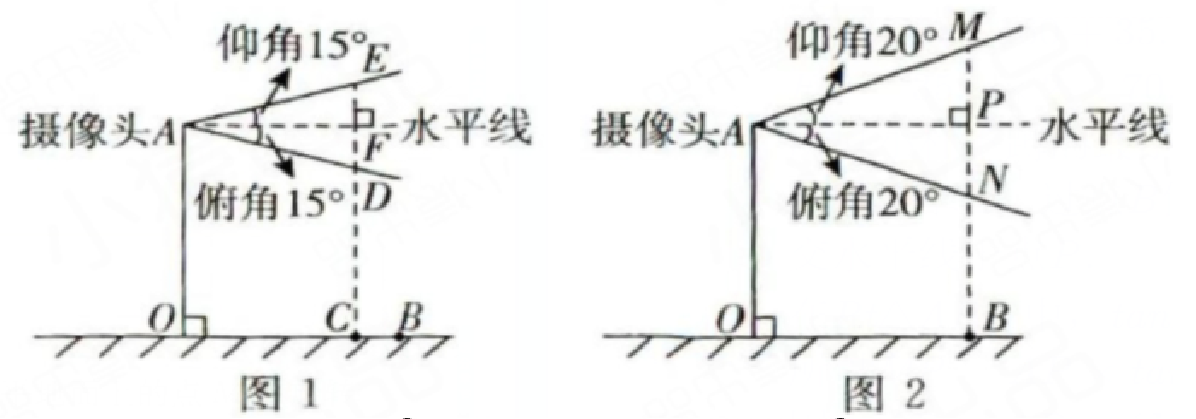
6. 某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别)的示意图如图①,摄像头 $ A $ 的仰角、俯角均为 $ 15^{\circ} $,摄像头距离地面的高度 $ OA = 160 \mathrm{~cm} $,识别的最远水平距离 $ OB = 150 \mathrm{~cm} $.
(1)小杜的身高为 $ 208 \mathrm{~cm} $,头部高度为 $ 26 \mathrm{~cm} $,他站在和摄像头水平距离为 $ 130 \mathrm{~cm} $ 的点 $ C $ 处,小杜最少需要下蹲多少厘米才能被识别?
(2)小若的身高为 $ 118 \mathrm{~cm} $,头部高度为 $ 15 \mathrm{~cm} $,踮起脚尖后增高 $ 5 \mathrm{~cm} $,但仍无法被识别.社区及时将摄像头的仰角、俯角都调整为 $ 20^{\circ} $(图②),此时小若能被识别吗?为什么?(精确到 $ 0.1 \mathrm{~cm} $;参考数据:$ \sin 15^{\circ} \approx 0.26 $,$ \cos 15^{\circ} \approx 0.97 $,$ \tan 15^{\circ} \approx 0.27 $,$ \sin 20^{\circ} \approx 0.34 $,$ \cos 20^{\circ} \approx 0.94 $,$ \tan 20^{\circ} \approx 0.36 $)

(1)小杜的身高为 $ 208 \mathrm{~cm} $,头部高度为 $ 26 \mathrm{~cm} $,他站在和摄像头水平距离为 $ 130 \mathrm{~cm} $ 的点 $ C $ 处,小杜最少需要下蹲多少厘米才能被识别?
(2)小若的身高为 $ 118 \mathrm{~cm} $,头部高度为 $ 15 \mathrm{~cm} $,踮起脚尖后增高 $ 5 \mathrm{~cm} $,但仍无法被识别.社区及时将摄像头的仰角、俯角都调整为 $ 20^{\circ} $(图②),此时小若能被识别吗?为什么?(精确到 $ 0.1 \mathrm{~cm} $;参考数据:$ \sin 15^{\circ} \approx 0.26 $,$ \cos 15^{\circ} \approx 0.97 $,$ \tan 15^{\circ} \approx 0.27 $,$ \sin 20^{\circ} \approx 0.34 $,$ \cos 20^{\circ} \approx 0.94 $,$ \tan 20^{\circ} \approx 0.36 $)

答案:
解:(1)如答图1,过点C作OB的垂线,
分别交仰角、俯角线于点E,D,交水平线于点F.
在Rt△AEF 中,$tan∠EAF=\frac {EF}{AF}$
所以$EF=AF×tan 15°≈130×0.27= 35.1(\ \mathrm {cm}). $
因为AF=AF,∠EAF=∠DAF,∠AFE=∠AFD= 90°,
所以$△ADF≌△AEF(\mathrm {ASA}),$
所以$EF= DF=35.1\ \mathrm {cm},$
所以$CE=160+35.1=195.1(\ \mathrm {cm}),$
$ED=35.1×2=70.2(\ \mathrm {cm})\gt 26\ \mathrm {cm},$
所以小杜下蹲的最小距离为$208-195. 1=12. 9(\ \mathrm {cm}).$
(2)如答图2,过点B作OB的垂线分别交仰角、俯角线于点M,N.
交水平线于点P.
在Rt△APM中,$tan∠MAP =\frac {MP}{AP}$
所以$MP=AP×tan 20°≈150×0.36= 54. 0(\ \mathrm {cm}).$
因为AP= AP,∠MAP=∠NAP,∠APM=∠APN=90°,
所以$△AMP≌△ANP(\mathrm {ASA}),$
所以$PN= MP= 54.0\ \mathrm {cm},$
所以$BN= 160- 54.0= 106.0(\ \mathrm {cm}).$
小若垫起脚尖后头顶的高度为$120+3= 123(\ \mathrm {cm}),$
所以小若头顶超出点N的高度$= 123- 106. 0= 17.0(\ \mathrm {cm})\gt 15(\ \mathrm {cm}),$
所以小若垫起脚尖后能被识别.
解:(1)如答图1,过点C作OB的垂线,
分别交仰角、俯角线于点E,D,交水平线于点F.
在Rt△AEF 中,$tan∠EAF=\frac {EF}{AF}$
所以$EF=AF×tan 15°≈130×0.27= 35.1(\ \mathrm {cm}). $
因为AF=AF,∠EAF=∠DAF,∠AFE=∠AFD= 90°,
所以$△ADF≌△AEF(\mathrm {ASA}),$
所以$EF= DF=35.1\ \mathrm {cm},$
所以$CE=160+35.1=195.1(\ \mathrm {cm}),$
$ED=35.1×2=70.2(\ \mathrm {cm})\gt 26\ \mathrm {cm},$
所以小杜下蹲的最小距离为$208-195. 1=12. 9(\ \mathrm {cm}).$
(2)如答图2,过点B作OB的垂线分别交仰角、俯角线于点M,N.
交水平线于点P.
在Rt△APM中,$tan∠MAP =\frac {MP}{AP}$
所以$MP=AP×tan 20°≈150×0.36= 54. 0(\ \mathrm {cm}).$
因为AP= AP,∠MAP=∠NAP,∠APM=∠APN=90°,
所以$△AMP≌△ANP(\mathrm {ASA}),$
所以$PN= MP= 54.0\ \mathrm {cm},$
所以$BN= 160- 54.0= 106.0(\ \mathrm {cm}).$
小若垫起脚尖后头顶的高度为$120+3= 123(\ \mathrm {cm}),$
所以小若头顶超出点N的高度$= 123- 106. 0= 17.0(\ \mathrm {cm})\gt 15(\ \mathrm {cm}),$
所以小若垫起脚尖后能被识别.
