4. 如图,小王在江边某瞭望台 $ D $处测得江面上渔船 $ A $的俯角为 $ 40^{\circ} $,若 $ DE = 3 \mathrm{m} $,$ CE = 2 \mathrm{m} $,$ CE $平行于江面 $ AB $,迎水坡 $ BC $的坡度 $ i = 1:0.75 $,坡长 $ BC = 10 \mathrm{m} $,则此时 $ AB $的长约为

5.1
m(精确到 $ 0.1 \mathrm{m} $).
答案:5.1
二、解答题
5. 某小区物业公司决定对小区环境进行优化改造.如图,$ AB $表示该小区一段长为 $ 20 \mathrm{m} $的斜坡,坡角 $ \angle BAD = 30^{\circ} $,$ BD ⊥ AD $,垂足为 $ D $.为方便通行,物业公司在不改变斜坡高度的情况下,把坡角降为 $ 15^{\circ} $.
(1) 求该斜坡的高度 $ BD $;
(2) 求斜坡新起点 $ C $与原起点 $ A $之间的距离.

5. 某小区物业公司决定对小区环境进行优化改造.如图,$ AB $表示该小区一段长为 $ 20 \mathrm{m} $的斜坡,坡角 $ \angle BAD = 30^{\circ} $,$ BD ⊥ AD $,垂足为 $ D $.为方便通行,物业公司在不改变斜坡高度的情况下,把坡角降为 $ 15^{\circ} $.
(1) 求该斜坡的高度 $ BD $;
(2) 求斜坡新起点 $ C $与原起点 $ A $之间的距离.

答案:解:(1)因为∠BAD=30°,BD⊥AD,AB=20m
所以$BD=\frac {1}{2}AB=10m$
(2)因为C,A,D三点共线,∠BAD=30°,∠ACB=15°
所以∠ABC=∠BAD-∠C=15°=∠C
所以AC=AB=20m
所以$BD=\frac {1}{2}AB=10m$
(2)因为C,A,D三点共线,∠BAD=30°,∠ACB=15°
所以∠ABC=∠BAD-∠C=15°=∠C
所以AC=AB=20m
6. 如图,斜坡 $ CD $的坡度 $ i = 1:2 $,在斜坡上有一棵垂直于水平面的大树 $ AB $.当太阳光与水平面的夹角为 $ 60^{\circ} $时,大树在斜坡上的影子 $ BE $长为 $ 10 \mathrm{m} $. 求大树 $ AB $的高.


答案:
解:过点E作EF⊥AB,交AB的延长线于点F
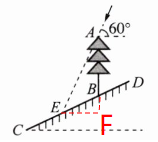
由题意得,∠AEF=60°,
∵斜坡CD的坡度i=1:2
∴$tan∠BEF=\frac{BF}{EF}=\frac{1}{2}$
∴EF=2BF,$BE=\sqrt{5}BF$
∵BE=10m
∴$BF=2\sqrt{5}m,$$EF=4\sqrt{5}m$
∵∠AEF=60°
∴$AF=EF·tan∠AEF=4\sqrt{5}×tan60°=4\sqrt{15}m$
∴$AB=AF-BF=(4\sqrt{15}-2\sqrt{5})m$
解:过点E作EF⊥AB,交AB的延长线于点F

由题意得,∠AEF=60°,
∵斜坡CD的坡度i=1:2
∴$tan∠BEF=\frac{BF}{EF}=\frac{1}{2}$
∴EF=2BF,$BE=\sqrt{5}BF$
∵BE=10m
∴$BF=2\sqrt{5}m,$$EF=4\sqrt{5}m$
∵∠AEF=60°
∴$AF=EF·tan∠AEF=4\sqrt{5}×tan60°=4\sqrt{15}m$
∴$AB=AF-BF=(4\sqrt{15}-2\sqrt{5})m$
7. 某兴趣小组开展了测量电线塔高度的实践活动.如图,斜坡 $ BE $的坡度 $ i = 1:\sqrt{3} $,$ BE = 6 \mathrm{m} $,在 $ B $处测得电线塔 $ CD $顶部 $ D $的仰角为 $ 45^{\circ} $,在 $ E $处测得电线塔 $ CD $顶部 $ D $的仰角为 $ 60^{\circ} $.求电线塔 $ CD $的高度.


答案:
解:如图,过点B作BF⊥CD,垂足为F,则四边形BACF为矩形.
由题意,得BA⊥AE.
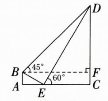
∵斜坡BE的坡度$i=1: \sqrt{3},$
∴在Rt△ABE中$,tan∠BEA=\frac{AB}{AE}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$
∴∠BEA=30°.
∵BE=6m,
∴易得$AB=\frac{1}{2}BE=3m.$
∴点B离水平地 面的高度AB为3m
∴AB=CF=3m,BF=AC.
设$EC=x\ \mathrm {m}$
∵在Rt△ABE中,
$AE=BE.cos{30}°=3\sqrt{3}\ \mathrm {m},$
∴$BF=AC=AE+CE=(x+3 \sqrt{3})m.$
∵ 在Rt△CDE中,∠DEC=60°,
∴$ CD=CE. tan{60}°= \sqrt{3} x\ \mathrm {m}$
∵ 在Rt△BDF 中,∠DBF=45°,
∴$ DF=BF.tan_{45}°=(x+3 \sqrt{3})m$
∵ DF+CF=CD,
∴$x+3 \sqrt{3}+3= \sqrt{3}x,$
解得$x=6+3 \sqrt{3}$
∴$ CD=(6\sqrt{3}+9)m.$
∴电线塔CD的高度为$(6\sqrt{3}+9)m .$
解:如图,过点B作BF⊥CD,垂足为F,则四边形BACF为矩形.
由题意,得BA⊥AE.

∵斜坡BE的坡度$i=1: \sqrt{3},$
∴在Rt△ABE中$,tan∠BEA=\frac{AB}{AE}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$
∴∠BEA=30°.
∵BE=6m,
∴易得$AB=\frac{1}{2}BE=3m.$
∴点B离水平地 面的高度AB为3m
∴AB=CF=3m,BF=AC.
设$EC=x\ \mathrm {m}$
∵在Rt△ABE中,
$AE=BE.cos{30}°=3\sqrt{3}\ \mathrm {m},$
∴$BF=AC=AE+CE=(x+3 \sqrt{3})m.$
∵ 在Rt△CDE中,∠DEC=60°,
∴$ CD=CE. tan{60}°= \sqrt{3} x\ \mathrm {m}$
∵ 在Rt△BDF 中,∠DBF=45°,
∴$ DF=BF.tan_{45}°=(x+3 \sqrt{3})m$
∵ DF+CF=CD,
∴$x+3 \sqrt{3}+3= \sqrt{3}x,$
解得$x=6+3 \sqrt{3}$
∴$ CD=(6\sqrt{3}+9)m.$
∴电线塔CD的高度为$(6\sqrt{3}+9)m .$