3. 若$\cos \alpha = \frac{\sqrt{2}}{2}$,则锐角$\alpha =$
$45^{\circ}$
;若$\tan (\beta - 30^{\circ}) = \frac{\sqrt{3}}{3}$,则锐角$\beta =$$60^{\circ}$
.答案:45°
60°
60°
4. 在$\triangle ABC$中,$\angle ABC = 90^{\circ}$,若$AC = 100$,$\sin A = \frac{3}{5}$,则$AB =$
80
.答案:80
5. 如图,已知等边三角形$ABC$内接于$\odot O$,$D$是劣弧$BC$上一点,则$\sin \angle ADB =$

$\frac{\sqrt{3}}{2}$
.
答案:$\frac {\sqrt{3}}{2}$
6. 如图,交警在高速公路上$A$处操控无人机巡查,无人机从$A$处飞行到$P$处悬停,探测到它正下方的公路上$B$处有汽车发生故障.已知$A$处到$P$处的距离为$500\ \mathrm{m}$,从$A$处观测$P$处的仰角为$\alpha$,且$\cos \alpha = 0.98$,则$A$处到$B$处的距离为

490
$\mathrm{m}$.
答案:6.490
解析:
解:在直角三角形$ABP$中,$\angle ABP = 90°$,$AP = 500\ \mathrm{m}$,$\cos\alpha = 0.98$。
因为$\cos\alpha=\frac{AB}{AP}$,所以$AB = AP·\cos\alpha = 500×0.98 = 490\ \mathrm{m}$。
490
因为$\cos\alpha=\frac{AB}{AP}$,所以$AB = AP·\cos\alpha = 500×0.98 = 490\ \mathrm{m}$。
490
7. 计算:
(1)$\sqrt{3} \tan 30^{\circ} + (3 - \pi)^0 + |1 - \sqrt{2}| - \sqrt{18}$;
(2)$\cos 60^{\circ} - 2 \sin^2 45^{\circ} + \frac{2}{3} \tan^2 60^{\circ} - \sin 30^{\circ}$.
(1)$\sqrt{3} \tan 30^{\circ} + (3 - \pi)^0 + |1 - \sqrt{2}| - \sqrt{18}$;
(2)$\cos 60^{\circ} - 2 \sin^2 45^{\circ} + \frac{2}{3} \tan^2 60^{\circ} - \sin 30^{\circ}$.
答案:7.(1)$1 - 2\sqrt{2}$;(2)1
解析:
(1)$\sqrt{3} \tan 30^{\circ} + (3 - \pi)^0 + |1 - \sqrt{2}| - \sqrt{18}$
$=\sqrt{3} × \frac{\sqrt{3}}{3} + 1 + (\sqrt{2} - 1) - 3\sqrt{2}$
$=1 + 1 + \sqrt{2} - 1 - 3\sqrt{2}$
$=1 - 2\sqrt{2}$
(2)$\cos 60^{\circ} - 2 \sin^2 45^{\circ} + \frac{2}{3} \tan^2 60^{\circ} - \sin 30^{\circ}$
$=\frac{1}{2} - 2 × (\frac{\sqrt{2}}{2})^2 + \frac{2}{3} × (\sqrt{3})^2 - \frac{1}{2}$
$=\frac{1}{2} - 2 × \frac{1}{2} + \frac{2}{3} × 3 - \frac{1}{2}$
$=\frac{1}{2} - 1 + 2 - \frac{1}{2}$
$=1$
$=\sqrt{3} × \frac{\sqrt{3}}{3} + 1 + (\sqrt{2} - 1) - 3\sqrt{2}$
$=1 + 1 + \sqrt{2} - 1 - 3\sqrt{2}$
$=1 - 2\sqrt{2}$
(2)$\cos 60^{\circ} - 2 \sin^2 45^{\circ} + \frac{2}{3} \tan^2 60^{\circ} - \sin 30^{\circ}$
$=\frac{1}{2} - 2 × (\frac{\sqrt{2}}{2})^2 + \frac{2}{3} × (\sqrt{3})^2 - \frac{1}{2}$
$=\frac{1}{2} - 2 × \frac{1}{2} + \frac{2}{3} × 3 - \frac{1}{2}$
$=\frac{1}{2} - 1 + 2 - \frac{1}{2}$
$=1$
8. 在$\triangle ABC$中,$\angle C = 90^{\circ}$,请根据下列条件解直角三角形.
(1)$\angle A = 30^{\circ}$,$a = 4\sqrt{3}$;
(2)$a = 6\sqrt{2}$,$c = 12$.
(1)$\angle A = 30^{\circ}$,$a = 4\sqrt{3}$;
(2)$a = 6\sqrt{2}$,$c = 12$.
答案:解: (1)在Rt△ABC中
因为∠A=30°,∠C=90°,∠B=60°
因为$a=4\sqrt{3}$
所以$b=\frac {a}{tan{30}°}=12,$$c=\frac {a}{sin{30}°}=8\sqrt{3}$
(2)在Rt△ABC中
因为$a= 6\sqrt{2},$c=12,∠C = 90°
所以$b=\sqrt{c²-a²}= 6\sqrt{2}$
所以$sinA=\frac {a}{c}=\frac {\sqrt{2}}{2},$$sinB=\frac {b}{c}=\frac {\sqrt{2}}{2}$
所以∠A=45°,∠B=45°
因为∠A=30°,∠C=90°,∠B=60°
因为$a=4\sqrt{3}$
所以$b=\frac {a}{tan{30}°}=12,$$c=\frac {a}{sin{30}°}=8\sqrt{3}$
(2)在Rt△ABC中
因为$a= 6\sqrt{2},$c=12,∠C = 90°
所以$b=\sqrt{c²-a²}= 6\sqrt{2}$
所以$sinA=\frac {a}{c}=\frac {\sqrt{2}}{2},$$sinB=\frac {b}{c}=\frac {\sqrt{2}}{2}$
所以∠A=45°,∠B=45°
9. 如图,在$\triangle ABC$中,$\angle C = 30^{\circ}$,点$D$在$AC$上,$DB ⊥ BC$,垂足为$B$,$AD:DC = 1:2$.求$\tan \angle ABD$.


答案:
解:过点A作AE⊥BD,交BD的延长线于点E ,如图所示
因为DB⊥BC, AE⊥DB
所以AE//BC,∠AED=∠DBC= 90°
所以∠EAD=∠C=30°,
所以△ADE∽△CDB
因为$\frac {AD}{DC}=\frac {1}{2}$
所以$\frac {AE}{BC}=\frac {DE}{DB}=\frac {1}{2}$
设DE=x ,则DB=2x, BE=3x
在Rt△ADE中
因为∠EAD=30°, DE=x
所以$AE=\sqrt{3}x$
所以$tan∠ABD=\frac {AE}{BE}=\frac {\sqrt{3}x}{3x}=\frac {\sqrt{3}}{3}$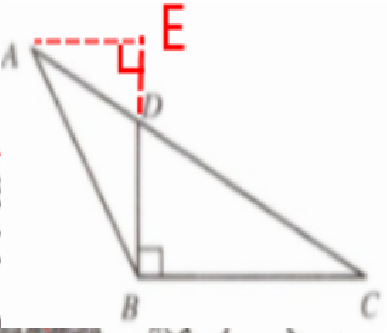
解:过点A作AE⊥BD,交BD的延长线于点E ,如图所示
因为DB⊥BC, AE⊥DB
所以AE//BC,∠AED=∠DBC= 90°
所以∠EAD=∠C=30°,
所以△ADE∽△CDB
因为$\frac {AD}{DC}=\frac {1}{2}$
所以$\frac {AE}{BC}=\frac {DE}{DB}=\frac {1}{2}$
设DE=x ,则DB=2x, BE=3x
在Rt△ADE中
因为∠EAD=30°, DE=x
所以$AE=\sqrt{3}x$
所以$tan∠ABD=\frac {AE}{BE}=\frac {\sqrt{3}x}{3x}=\frac {\sqrt{3}}{3}$
