10. 公园一座塔楼的剖面和台阶的剖面在同一平面,在台阶底部点$A$处测得塔楼顶端点$E$的仰角$\angle EAG = 45^{\circ}$,台阶$AB$长$26\ \mathrm{m}$,台阶坡面$AB$的坡度$i = 5:12$;在点$B$处测得塔楼顶端点$E$的仰角$\angle EBF = 60^{\circ}$.塔顶到地面的高度$EF$为多少?


答案:
解:过B作AG垂线于C
因为AB的坡度为i=5:12
所以设BC=5x,AC=12x
因为AB=26m
所以(5x)²+(12x)²=26²
所以x=2
所以BC=10m,AC=24m
因为∠EBF=60°
所以设BF=x,$EF=\sqrt{3}x$
因为∠RAG=45°
根据题意可得:$\sqrt{3}x+10=x+24$
$(\sqrt{3}-1)x=14$
$x=7(\sqrt{3}+1)$
所以$EF=\sqrt{3}x=7\sqrt{3}(\sqrt{3}+1)=21+7\sqrt{3}m$
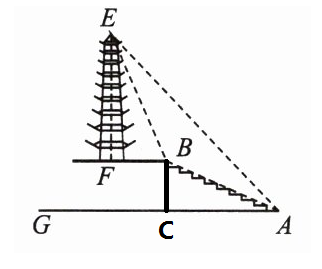
解:过B作AG垂线于C
因为AB的坡度为i=5:12
所以设BC=5x,AC=12x
因为AB=26m
所以(5x)²+(12x)²=26²
所以x=2
所以BC=10m,AC=24m
因为∠EBF=60°
所以设BF=x,$EF=\sqrt{3}x$
因为∠RAG=45°
根据题意可得:$\sqrt{3}x+10=x+24$
$(\sqrt{3}-1)x=14$
$x=7(\sqrt{3}+1)$
所以$EF=\sqrt{3}x=7\sqrt{3}(\sqrt{3}+1)=21+7\sqrt{3}m$

11. 如图,在建筑物$AB$和$CD$的楼顶之间悬挂彩带,彩带用线段$AD$表示.在点$A$测得点$C$的俯角为$23.8^{\circ}$,点$D$的仰角为$36.9^{\circ}$.已知$AB = 13.20\ \mathrm{m}$,求$AD$的长.(精确到$0.1\ \mathrm{m}$,参考数据:$\sin 23.8^{\circ} \approx 0.40$,$\cos 23.8^{\circ} \approx 0.91$,$\tan 23.8^{\circ} \approx 0.44$,$\sin 36.9^{\circ} \approx 0.60$,$\cos 36.9^{\circ} \approx 0.80$,$\tan 36.9^{\circ} \approx 0.75$)


答案:11.$37.5\mathrm{ m}$
解析:
解:过点$A$作$AE ⊥ CD$于点$E$,则四边形$ABCE$为矩形,$AE = BC$,$EC = AB = 13.20\ \mathrm{m}$。
设$AE = x\ \mathrm{m}$,在$\mathrm{Rt}\triangle AEC$中,$\angle CAE = 23.8^{\circ}$,$\tan 23.8^{\circ} = \dfrac{EC}{AE}$,即$0.44 = \dfrac{13.20}{x}$,解得$x = 30\ \mathrm{m}$。
在$\mathrm{Rt}\triangle AED$中,$\angle DAE = 36.9^{\circ}$,$\cos 36.9^{\circ} = \dfrac{AE}{AD}$,即$0.80 = \dfrac{30}{AD}$,解得$AD = 37.5\ \mathrm{m}$。
答:$AD$的长为$37.5\ \mathrm{m}$。
设$AE = x\ \mathrm{m}$,在$\mathrm{Rt}\triangle AEC$中,$\angle CAE = 23.8^{\circ}$,$\tan 23.8^{\circ} = \dfrac{EC}{AE}$,即$0.44 = \dfrac{13.20}{x}$,解得$x = 30\ \mathrm{m}$。
在$\mathrm{Rt}\triangle AED$中,$\angle DAE = 36.9^{\circ}$,$\cos 36.9^{\circ} = \dfrac{AE}{AD}$,即$0.80 = \dfrac{30}{AD}$,解得$AD = 37.5\ \mathrm{m}$。
答:$AD$的长为$37.5\ \mathrm{m}$。
12. 如图①,院子里有一个晾衣装置,立柱$AB$和$CD$分别垂直于地面$l$,垂足分别为$B$、$D$,$AB = 19\ \mathrm{dm}$,$CD > AB$.在点$A$、$C$之间的晾衣绳上有固定挂钩$E$,$AE = 13\ \mathrm{dm}$,小丽把一件连衣裙$MN$挂在点$E$处(点$M$与点$E$重合),发现$MN ⊥ l$.且当这件连衣裙下端点$N$刚好接触到地面$l$时,点$E$到直线$AB$的距离$EG = 12\ \mathrm{dm}$.
(1)求这件连衣裙$MN$的长.
(2)如图②,为避免该连衣裙接触到地面,小丽在另一个固定挂钩$F$处又挂了一条长裤(点$F$在点$E$的右侧).若$\angle BAE = 76.1^{\circ}$,求此时该连衣裙下端点$N$到地面水平线$l$的距离.(参考数据:$\sin 76.1^{\circ} \approx 0.97$,$\cos 76.1^{\circ} \approx 0.24$,$\tan 76.1^{\circ} \approx 4.04$)

(1)求这件连衣裙$MN$的长.
(2)如图②,为避免该连衣裙接触到地面,小丽在另一个固定挂钩$F$处又挂了一条长裤(点$F$在点$E$的右侧).若$\angle BAE = 76.1^{\circ}$,求此时该连衣裙下端点$N$到地面水平线$l$的距离.(参考数据:$\sin 76.1^{\circ} \approx 0.97$,$\cos 76.1^{\circ} \approx 0.24$,$\tan 76.1^{\circ} \approx 4.04$)

答案:12.(1)$14\mathrm{ dm}$;(2)$1.88\mathrm{ dm}$
解析:
(1)解:在$Rt\triangle AGE$中,$AE=13\ \mathrm{dm}$,$EG=12\ \mathrm{dm}$,由勾股定理得$AG=\sqrt{AE^{2}-EG^{2}}=\sqrt{13^{2}-12^{2}}=5\ \mathrm{dm}$。
因为$AB=19\ \mathrm{dm}$,所以$MN=AB - AG=19 - 5=14\ \mathrm{dm}$。
(2)解:在$Rt\triangle AGE$中,$\sin\angle BAE=\frac{EG}{AE}$,则$EG=AE·\sin\angle BAE\approx13×0.97=12.61\ \mathrm{dm}$。
$\cos\angle BAE=\frac{AG}{AE}$,则$AG=AE·\cos\angle BAE\approx13×0.24=3.12\ \mathrm{dm}$。
连衣裙下端点$N$到地面$l$的距离为$AB - AG - MN=19 - 3.12 - 14=1.88\ \mathrm{dm}$。
因为$AB=19\ \mathrm{dm}$,所以$MN=AB - AG=19 - 5=14\ \mathrm{dm}$。
(2)解:在$Rt\triangle AGE$中,$\sin\angle BAE=\frac{EG}{AE}$,则$EG=AE·\sin\angle BAE\approx13×0.97=12.61\ \mathrm{dm}$。
$\cos\angle BAE=\frac{AG}{AE}$,则$AG=AE·\cos\angle BAE\approx13×0.24=3.12\ \mathrm{dm}$。
连衣裙下端点$N$到地面$l$的距离为$AB - AG - MN=19 - 3.12 - 14=1.88\ \mathrm{dm}$。