13. 如图,在矩形$ABCD$中,$E$、$F$是边$BC$上两点,且$BE = EF = FC$,连接$DE$、$AF$,$DE$与$AF$相交于点$G$,连接$BG$.若$AB = 4$,$BC = 6$,则$\sin \angle GBF$的值为

$\frac{\sqrt{10}}{10}$
.
答案:
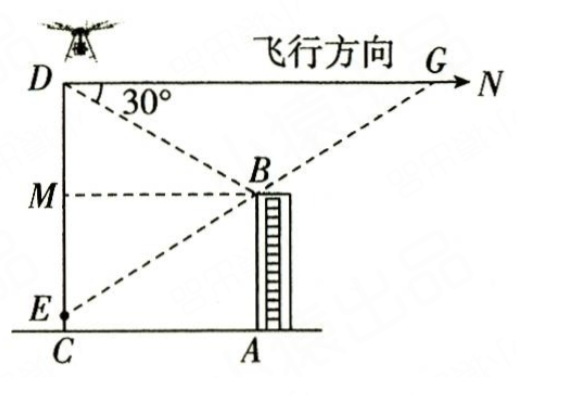
解:(1)如图,过点B作BM⊥CD于点M,
则∠DBM=∠BDN=30°.
在Rt△BDM中,$BM=AC=243\ \mathrm {m},$ ∠DBM = 30°,
所以$DM= BM×tan∠DBM=24\sqrt{3}×\frac {\sqrt{3}}{3}=24(\mathrm {m}) $
所以$AB=CM=CD-DM=49.6-24=25. 6(\mathrm {m}).$
答:教学楼AB的高度为$25.6\ \mathrm {m}.$
(2)如图,连接EB并延长交DN于点G,
则∠DGE=∠MBE.
在Rt△EMB中,$BM =AC =24\sqrt{3}m,$$ EM =CM-CE=24\ \mathrm {m},$
所以$ tan∠MBE=\frac {EM}{BM}=\frac {24}{24\sqrt{3}}=\frac {\sqrt{3}}{3}. $
所以∠MBE=30°=∠DGE.
因为∠EDG=90°.
所以∠DEG =90° - 30° = 60°.
在Rt△EDG 中,$DE=CD-CE=48\ \mathrm {m},$
所以$DG=DE×tan 60° =48\sqrt{3}m.$
$48\sqrt{3}÷4\sqrt{3}=12(\mathrm {s}).$
所以经过$12\ \mathrm {s}$时,无人机刚好离开了圆圆的视线.
$ \frac{\sqrt{10}}{10}$
解:(1)如图,过点B作BM⊥CD于点M,
则∠DBM=∠BDN=30°.
在Rt△BDM中,$BM=AC=243\ \mathrm {m},$ ∠DBM = 30°,
所以$DM= BM×tan∠DBM=24\sqrt{3}×\frac {\sqrt{3}}{3}=24(\mathrm {m}) $
所以$AB=CM=CD-DM=49.6-24=25. 6(\mathrm {m}).$
答:教学楼AB的高度为$25.6\ \mathrm {m}.$
(2)如图,连接EB并延长交DN于点G,
则∠DGE=∠MBE.
在Rt△EMB中,$BM =AC =24\sqrt{3}m,$$ EM =CM-CE=24\ \mathrm {m},$
所以$ tan∠MBE=\frac {EM}{BM}=\frac {24}{24\sqrt{3}}=\frac {\sqrt{3}}{3}. $
所以∠MBE=30°=∠DGE.
因为∠EDG=90°.
所以∠DEG =90° - 30° = 60°.
在Rt△EDG 中,$DE=CD-CE=48\ \mathrm {m},$
所以$DG=DE×tan 60° =48\sqrt{3}m.$
$48\sqrt{3}÷4\sqrt{3}=12(\mathrm {s}).$
所以经过$12\ \mathrm {s}$时,无人机刚好离开了圆圆的视线.

$ \frac{\sqrt{10}}{10}$
14. 如图为《天工开物》记载的用于春捣谷物的工具——“碓”的示意图.已知$AB ⊥ CD$,垂足为$B$,$AB$与水平线$l$相交于点$O$,$OE ⊥ l$.若$BC = 4\ \mathrm{dm}$,$OB = 12\ \mathrm{dm}$,$\angle BOE = 60^{\circ}$,则点$C$到水平线$l$的距离$CF$为

$6 - 2\sqrt{3}$
$\mathrm{dm}$.
答案:$ (6-2\sqrt{3})$
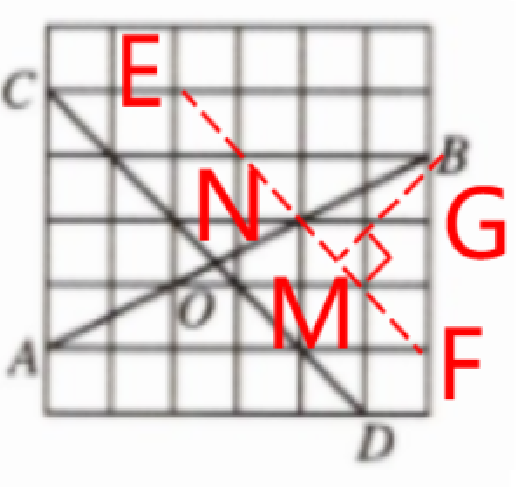
15. 在如图的正方形方格纸中,$A$、$B$、$C$、$D$都在格点处,$AB$与$CD$相交于点$O$,试求$\tan \angle BOD$的值.


答案:
解:作EF//CD ,过点B作BM⊥EF ,垂足为点M ,如图所示
设正方形方格纸每一小格的边长为a ,
则NG= 2a, BF=3a ,$ BN=\sqrt{(2a)²+a²}=\sqrt{5}a$
因为NG=2a,BF=3a
所以$S_{△BFN}=\frac {1}{2}×NG×BF=3a²$
因为$NF=\sqrt{NG²+FG²}=2\sqrt{2}a,$
$S_{△BFN}=\frac {1}{2}×NF×BM$
所以$BM =\frac {2S_{△BFN}}{NF}=\frac {6a²}{2\sqrt{2}a}=\frac {3\sqrt{2}a}{2}$
所以$MN= \sqrt{BN²-BM²}=\frac {\sqrt{2}}{2}a$
因为EF//CD
所以∠BOD=∠BNM
所以$tan∠BOD = tan∠BNM =\frac {BN}{NM}=3$
解:作EF//CD ,过点B作BM⊥EF ,垂足为点M ,如图所示
设正方形方格纸每一小格的边长为a ,
则NG= 2a, BF=3a ,$ BN=\sqrt{(2a)²+a²}=\sqrt{5}a$
因为NG=2a,BF=3a
所以$S_{△BFN}=\frac {1}{2}×NG×BF=3a²$
因为$NF=\sqrt{NG²+FG²}=2\sqrt{2}a,$
$S_{△BFN}=\frac {1}{2}×NF×BM$
所以$BM =\frac {2S_{△BFN}}{NF}=\frac {6a²}{2\sqrt{2}a}=\frac {3\sqrt{2}a}{2}$
所以$MN= \sqrt{BN²-BM²}=\frac {\sqrt{2}}{2}a$
因为EF//CD
所以∠BOD=∠BNM
所以$tan∠BOD = tan∠BNM =\frac {BN}{NM}=3$

16. 某晚,小宇在家通过窗户的最高点$P$恰好看到一颗星星,此时小宇距窗户的水平距离$BQ = 4\ \mathrm{m}$,仰角为$\alpha$;小宇向前走了$3\ \mathrm{m}$后到达点$D$,通过点$P$恰好看到月亮,仰角为$\beta$,如图.已知,小宇的眼睛与水平地面$BQ$的距离$AB = CD = 1.6\ \mathrm{m}$,点$P$到$BQ$的距离$PQ = 2.6\ \mathrm{m}$,$AC$的延长线交$PQ$于点$E$.
(1)求$\beta$的大小及$\tan \alpha$的值;
(2)求$CP$的长及$\sin \angle APC$的值.

(1)求$\beta$的大小及$\tan \alpha$的值;
(2)求$CP$的长及$\sin \angle APC$的值.

答案:解:(1)由题意,得PQ⊥AE,PQ=2.6m,
AB=CD=EQ=1.6m,AE=BQ=4m,
AC=BD=3m,
∴CE=1m,PE=1m,∠CEP=90°,
∴CE=PE,
∴$β=∠PCE=45°,tanα=tan∠PAE=\frac{PE}{AE}=\frac{1}{4}$
(2)
∵CE=PE=1m,∠CEP=90°,
∴$CP=\sqrt{2}m$过点C作CH⊥AP于点H.
∵$tanα=tan∠PAE=\frac{CH}{AH}=\frac{1}{4},$
∴设CH=xm,则AH=4xm,
在Rt△AHC中,x²+(4x)²=AC²=9,
解得$x=\frac{3\sqrt{17}}{17}($负值已舍去),
∴$CH=\frac{3\sqrt{17}}{17}m$
∴$sin∠APC=\frac{CH}{CP}=\frac{\frac{3\sqrt{17}}{17}}{\sqrt{2}}=\frac{3\sqrt{34}}{34}.$
AB=CD=EQ=1.6m,AE=BQ=4m,
AC=BD=3m,
∴CE=1m,PE=1m,∠CEP=90°,
∴CE=PE,
∴$β=∠PCE=45°,tanα=tan∠PAE=\frac{PE}{AE}=\frac{1}{4}$
(2)
∵CE=PE=1m,∠CEP=90°,
∴$CP=\sqrt{2}m$过点C作CH⊥AP于点H.
∵$tanα=tan∠PAE=\frac{CH}{AH}=\frac{1}{4},$
∴设CH=xm,则AH=4xm,
在Rt△AHC中,x²+(4x)²=AC²=9,
解得$x=\frac{3\sqrt{17}}{17}($负值已舍去),
∴$CH=\frac{3\sqrt{17}}{17}m$
∴$sin∠APC=\frac{CH}{CP}=\frac{\frac{3\sqrt{17}}{17}}{\sqrt{2}}=\frac{3\sqrt{34}}{34}.$