17. 为了解渔船海上作业情况,某日,数学兴趣小组开展了实践活动.如图,一艘渔船以$10\ \mathrm{n mile/h}$的速度自东向西向码头$A$航行,小组同学收集到以下信息:


请根据以上信息,解答下列问题:
(1)求渔船在航行过程中与灯塔$B$的最短距离;
(2)若不改变航行速度,请通过计算说明,渔船能否在浓雾到来前到达码头$A$.(参考数据:$\sin 37^{\circ} \approx 0.60$,$\cos 37^{\circ} \approx 0.80$,$\tan 37^{\circ} \approx 0.75$,$\sin 14^{\circ} \approx 0.24$,$\cos 14^{\circ} \approx 0.97$,$\tan 14^{\circ} \approx 0.25$)


请根据以上信息,解答下列问题:
(1)求渔船在航行过程中与灯塔$B$的最短距离;
(2)若不改变航行速度,请通过计算说明,渔船能否在浓雾到来前到达码头$A$.(参考数据:$\sin 37^{\circ} \approx 0.60$,$\cos 37^{\circ} \approx 0.80$,$\tan 37^{\circ} \approx 0.75$,$\sin 14^{\circ} \approx 0.24$,$\cos 14^{\circ} \approx 0.97$,$\tan 14^{\circ} \approx 0.25$)
答案:17.(1)$15\mathrm{ n mile}$;(2)能
解析:
(1)过点$B$作$BC ⊥ AD$于点$C$,设$BC = x\ \mathrm{n mile}$。
在$\mathrm{Rt}\triangle BCD$中,$\angle BDC = 37^{\circ}$,$\tan 37^{\circ} = \frac{BC}{CD}$,则$CD = \frac{BC}{\tan 37^{\circ}} \approx \frac{x}{0.75}$。
在$\mathrm{Rt}\triangle BCA$中,$\angle BAC = 14^{\circ}$,$\tan 14^{\circ} = \frac{BC}{AC}$,则$AC = \frac{BC}{\tan 14^{\circ}} \approx \frac{x}{0.25}$。
由题意得$AD = AC - CD = 40\ \mathrm{n mile}$,即$\frac{x}{0.25} - \frac{x}{0.75} = 40$,解得$x = 15$。
渔船与灯塔$B$的最短距离为$15\ \mathrm{n mile}$。
(2)由(1)知$AC = \frac{15}{0.25} = 60\ \mathrm{n mile}$,渔船速度为$10\ \mathrm{n mile/h}$,所需时间$t = \frac{60}{10} = 6\ \mathrm{h}$。
因为$6\ \mathrm{h} < 7\ \mathrm{h}$,所以能在浓雾到来前到达码头$A$。
(1)$15\ \mathrm{n mile}$;(2)能
在$\mathrm{Rt}\triangle BCD$中,$\angle BDC = 37^{\circ}$,$\tan 37^{\circ} = \frac{BC}{CD}$,则$CD = \frac{BC}{\tan 37^{\circ}} \approx \frac{x}{0.75}$。
在$\mathrm{Rt}\triangle BCA$中,$\angle BAC = 14^{\circ}$,$\tan 14^{\circ} = \frac{BC}{AC}$,则$AC = \frac{BC}{\tan 14^{\circ}} \approx \frac{x}{0.25}$。
由题意得$AD = AC - CD = 40\ \mathrm{n mile}$,即$\frac{x}{0.25} - \frac{x}{0.75} = 40$,解得$x = 15$。
渔船与灯塔$B$的最短距离为$15\ \mathrm{n mile}$。
(2)由(1)知$AC = \frac{15}{0.25} = 60\ \mathrm{n mile}$,渔船速度为$10\ \mathrm{n mile/h}$,所需时间$t = \frac{60}{10} = 6\ \mathrm{h}$。
因为$6\ \mathrm{h} < 7\ \mathrm{h}$,所以能在浓雾到来前到达码头$A$。
(1)$15\ \mathrm{n mile}$;(2)能
18. 如图①,塑像$AB$在底座$BC$上,点$D$是人眼所在的位置.当点$B$高于人的水平视线$DE$时,由远及近看塑像,会在某处感觉看到的塑像最大,此时视角最大.研究发现:当经过$A$,$B$两点的圆与水平视线$DE$相切时(图②),在切点$P$处感觉看到的塑像最大,此时$\angle APB$为最大视角.
(1)请仅就图②的情形证明$\angle APB > \angle ADB$;
(2)经测量,最大视角$\angle APB = 30^{\circ}$,在点$P$处看塑像顶部点$A$的仰角$\angle APE = 60^{\circ}$,点$P$到塑像的水平距离$PH$为$6\ \mathrm{m}$.求塑像$AB$的高.

(1)请仅就图②的情形证明$\angle APB > \angle ADB$;
(2)经测量,最大视角$\angle APB = 30^{\circ}$,在点$P$处看塑像顶部点$A$的仰角$\angle APE = 60^{\circ}$,点$P$到塑像的水平距离$PH$为$6\ \mathrm{m}$.求塑像$AB$的高.

答案:
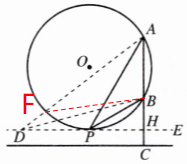
解:(1)设AD与⊙O交于点F,连接BF
∵∠APB=∠AFB
又
∵∠AFB=∠ADB+∠DBF>∠ADB
∴∠APB>∠ADB
(2)由题意得,DE⊥AC
∵∠APE=60°,PH=6m
∴$AH=PH·tan∠APE=6×tan60°=6\sqrt{3}m$
∵∠APB=30°
∴∠BPH=30°
∴$BH=PH·tan∠BPH=6×tan30°=2\sqrt{3}m$
∴$AB=AH-BH=6\sqrt{3}-2\sqrt{3}=4\sqrt{3}m$

解:(1)设AD与⊙O交于点F,连接BF
∵∠APB=∠AFB
又
∵∠AFB=∠ADB+∠DBF>∠ADB
∴∠APB>∠ADB
(2)由题意得,DE⊥AC
∵∠APE=60°,PH=6m
∴$AH=PH·tan∠APE=6×tan60°=6\sqrt{3}m$
∵∠APB=30°
∴∠BPH=30°
∴$BH=PH·tan∠BPH=6×tan30°=2\sqrt{3}m$
∴$AB=AH-BH=6\sqrt{3}-2\sqrt{3}=4\sqrt{3}m$