7. 已知$\triangle ABC$的三边长分别为$1$、$\sqrt{3}$、$\sqrt{2}$,$\triangle A'B'C'$的两边长分别为$\sqrt{2}$和$\sqrt{6}$. 如果$\triangle ABC\backsim\triangle A'B'C'$,那么$\triangle A'B'C'$的第三边为
2
.答案:2
8. 下列条件中,不能使$\triangle ABC$和$\triangle DEF$相似的是(
A.$\angle A=\angle D = 45^{\circ}38'$,$\angle C = 26^{\circ}22'$,$\angle E = 108^{\circ}$
B.$AB = 1$,$AC = 1.5$,$BC = 2$,$DE = 12$,$EF = 8$,$DF = 16$
C.$BC = a$,$AC = b$,$AB = c$,$DE = \sqrt{a}$,$EF = \sqrt{b}$,$DF = \sqrt{c}$
D.$AB = AC$,$DE = DF$,$\angle A=\angle D = 40^{\circ}$
C
).A.$\angle A=\angle D = 45^{\circ}38'$,$\angle C = 26^{\circ}22'$,$\angle E = 108^{\circ}$
B.$AB = 1$,$AC = 1.5$,$BC = 2$,$DE = 12$,$EF = 8$,$DF = 16$
C.$BC = a$,$AC = b$,$AB = c$,$DE = \sqrt{a}$,$EF = \sqrt{b}$,$DF = \sqrt{c}$
D.$AB = AC$,$DE = DF$,$\angle A=\angle D = 40^{\circ}$
答案:C
9. 已知:如图,$AG$、$DH$分别是$\triangle ABC$和$\triangle DEF$的角平分线,且$\frac{AB}{DE}=\frac{BG}{EH}=\frac{AG}{DH}$.
求证:$\triangle DEF\backsim\triangle ABC$.

求证:$\triangle DEF\backsim\triangle ABC$.

答案:证明:∵$\frac {AB}{DE}=\frac {BG}{EH}=\frac {AG}{DH}$
∴△ABG∽△DEH
∴∠BAG=∠EDH,∠B=∠E
∵AG、DH分别是角平分线
∴∠BAC=2∠BAG,∠EDF=2∠EDH
∴∠BAC=∠EDF
∵∠B=∠E
∴△DEF∽△ABC
∴△ABG∽△DEH
∴∠BAG=∠EDH,∠B=∠E
∵AG、DH分别是角平分线
∴∠BAC=2∠BAG,∠EDF=2∠EDH
∴∠BAC=∠EDF
∵∠B=∠E
∴△DEF∽△ABC
10. 如图,由三个小正方形拼成一个矩形$AEDF$. 请你猜想$\angle 1$、$\angle 2$、$\angle 3$有什么关系,并说明你的猜想是正确的.


答案:解:猜想∠1+∠2=∠3
∵$\frac {BC}{AB}=\frac {AB}{BD}=\frac {\sqrt 2}2,$∠ABC=∠DBA
∴△ABC∽△DBA
∴∠1=∠BAC
∵∠BAC+∠2=∠3
∴∠1+∠2=∠3
∵$\frac {BC}{AB}=\frac {AB}{BD}=\frac {\sqrt 2}2,$∠ABC=∠DBA
∴△ABC∽△DBA
∴∠1=∠BAC
∵∠BAC+∠2=∠3
∴∠1+∠2=∠3
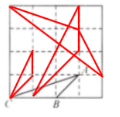
11. 如图,在$4×4$的正方形方格中,$\triangle ABC$的顶点都在边长为$1$的小正方形的顶点上(称为格点三角形). 在图中画出所有与$\triangle ABC$相似且相似比不为$1$的格点三角形,并说明理由.


答案:
解:如图所示,因为图中的格点三角形与△ABC的三边成比例,
所以图中的三个格点三角形与△ABC相似。
解:如图所示,因为图中的格点三角形与△ABC的三边成比例,
所以图中的三个格点三角形与△ABC相似。
