6. 如图,在坡角为$30^{\circ}$的坡面$AB$上等距离地植树,要使相邻两棵树的水平距离都为$3\mathrm{m}$,那么相邻两棵树间的坡面距离应为(

A.$6\mathrm{m}$
B.$\sqrt{3}\mathrm{m}$
C.$2\sqrt{3}\mathrm{m}$
D.$2\sqrt{2}\mathrm{m}$
C
).
A.$6\mathrm{m}$
B.$\sqrt{3}\mathrm{m}$
C.$2\sqrt{3}\mathrm{m}$
D.$2\sqrt{2}\mathrm{m}$
答案:C
7. 如图,直角三角形纸片的两直角边长分别为$6$、$8$,将$\triangle ABC$折叠,使点$A$与点$B$重合,折痕为$DE$,则$\tan\angle CBE$的值是(

A.$\frac{24}{7}$
B.$\frac{\sqrt{7}}{3}$
C.$\frac{7}{24}$
D.$\frac{1}{3}$
C
).
A.$\frac{24}{7}$
B.$\frac{\sqrt{7}}{3}$
C.$\frac{7}{24}$
D.$\frac{1}{3}$
答案:C
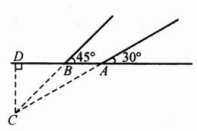
8. 在某次地震救援行动中,救援队利用生命探测仪在地面$A$、$B$两个探测点探测到$C$处有生命迹象(如图). 已知$A$、$B$两点相距$4\mathrm{m}$,探测线与地面的夹角分别是$30^{\circ}$和$45^{\circ}$,试确定点$C$距地面的深度(精确到$0.1\mathrm{m}$).


答案:
解:过点C作CD⊥AB,垂足为D
设CD=x
在Rt△ACD中,∠CAD=30°,
则$AD=\sqrt 3CD=\sqrt{3} x$
在Rt△BCD中,∠CBD=45°,
则BD=CD=x
由题意,得$\sqrt 3x-x=4$
解得$x=\frac {4}{\sqrt 3-1}=2( \sqrt{3}+1)≈5.5$
∴点C距地面的深度为$5.5\ \mathrm {m}\ $
解:过点C作CD⊥AB,垂足为D

设CD=x
在Rt△ACD中,∠CAD=30°,
则$AD=\sqrt 3CD=\sqrt{3} x$
在Rt△BCD中,∠CBD=45°,
则BD=CD=x
由题意,得$\sqrt 3x-x=4$
解得$x=\frac {4}{\sqrt 3-1}=2( \sqrt{3}+1)≈5.5$
∴点C距地面的深度为$5.5\ \mathrm {m}\ $
9. 如图,景区湖中有一小岛,湖边有一条笔直的观光道$AB$,现要从小岛上的点$P$处架一座与观光道垂直的小桥$PD$,将小岛与观光道连接. 已知在观光道上测得如下数据:$AB = 80.0\mathrm{m}$,$\angle PAB = 38.5^{\circ}$,$\angle PBA = 26.5^{\circ}$,求小桥的长度$PD$(精确到$0.1\mathrm{m}$. 参考数据:$\sin 38.5^{\circ} \approx 0.62$,$\cos 38.5^{\circ} \approx 0.78$,$\tan 38.5^{\circ} \approx 0.80$,$\sin 26.5^{\circ} \approx 0.45$,$\cos 26.5^{\circ} \approx 0.89$,$\tan 26.5^{\circ} \approx 0.50$).


答案:解:设PD=xm
∵PD⊥AB
∴∠ADP=∠BDP=90°
在Rt △PAD中,$tan ∠PAD=\frac {x}{AD}$
∴$AD= \frac x{tan 38.5°}≈ \frac {x}{0.80}=1.25x$
在 Rt △PBD中,$tan ∠PBD=\frac {x}{DB}$
∴$DB=\frac {x}{tan 26.5°} ≈ \frac {x}{0.50}=2x$
又∵$AB=80.0\ \mathrm {m}$
∴1.25x+2x=80.0
解得x≈24.6,即$PD≈24.6\ \mathrm {m}$
∵PD⊥AB
∴∠ADP=∠BDP=90°
在Rt △PAD中,$tan ∠PAD=\frac {x}{AD}$
∴$AD= \frac x{tan 38.5°}≈ \frac {x}{0.80}=1.25x$
在 Rt △PBD中,$tan ∠PBD=\frac {x}{DB}$
∴$DB=\frac {x}{tan 26.5°} ≈ \frac {x}{0.50}=2x$
又∵$AB=80.0\ \mathrm {m}$
∴1.25x+2x=80.0
解得x≈24.6,即$PD≈24.6\ \mathrm {m}$