1. (2025·启东期中)如图,在平面直角坐标系中,直线 $ AB $ 与 $ x $ 轴交于点 $ A(-3,0) $,与 $ y $ 轴交于点 $ B $,与直线 $ OC $ 相交于点 $ C(-2,1) $,点 $ M $ 在直线 $ AB $ 上运动.
(1) 求直线 $ AB $ 对应的函数解析式.
(2) 是否存在点 $ M $,使 $ \triangle OMB $ 的面积是 $ \triangle OBC $ 面积的 $ \frac{1}{2} $? 若存在,求出此时点 $ M $ 的坐标;若不存在,请说明理由.
(3) 若点 $ P $ 在 $ y $ 轴上,在坐标平面内是否存在点 $ Q $,使得以 $ A,B,P,Q $ 为顶点的四边形是菱形?若存在,求出点 $ Q $ 的坐标;若不存在,请说明理由.
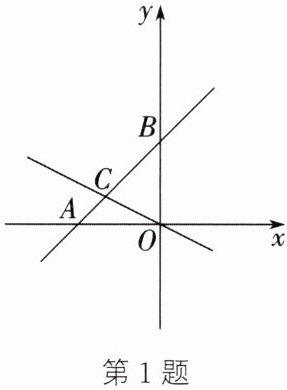
(1) 求直线 $ AB $ 对应的函数解析式.
(2) 是否存在点 $ M $,使 $ \triangle OMB $ 的面积是 $ \triangle OBC $ 面积的 $ \frac{1}{2} $? 若存在,求出此时点 $ M $ 的坐标;若不存在,请说明理由.
(3) 若点 $ P $ 在 $ y $ 轴上,在坐标平面内是否存在点 $ Q $,使得以 $ A,B,P,Q $ 为顶点的四边形是菱形?若存在,求出点 $ Q $ 的坐标;若不存在,请说明理由.

答案:
1.(1)设直线AB对应的函数解析式为$y=kx+b$.将$A(-3,0),C(-2,1)$代入,得$\begin{cases}0=-3k+b,\\1=-2k+b.\end{cases}$解得$\begin{cases}k=1,\\b=3.\end{cases}$
∴直线AB对应的函数解析式为$y=x+3$
(2)存在.
∵直线AB对应的函数解析式为$y=x+3$,
∴令$x=0$,则$y=3$.
∴$B(0,3)$,即$OB=3$.
∵$C(-2,1)$,
∴$S_{\triangle OBC}=\frac{1}{2}OB·|-2|=\frac{1}{2}×3×2=3$.
∴$S_{\triangle OMB}=\frac{3}{2}$.设$M(a,a+3)$.
∴$S_{\triangle OMB}=\frac{1}{2}OB·|a|=\frac{1}{2}×3×|a|=\frac{3}{2}|a|=\frac{3}{2}$,解得$a=-1$或$a=1$.
∴$M(1,4)$或$(-1,2)$
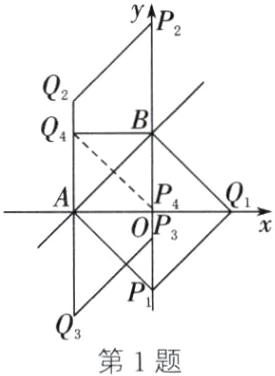
(3)存在.
∵$A(-3,0),B(0,3)$,
∴$AB=\sqrt{3^2+3^2}=3\sqrt{2}$.如图.①当$AB$是菱形的一条边时,点$P_1$与点$B$关于$x$轴对称时,$Q_1(3,0)$是点$A$关于$y$轴的对称点,四边形$ABQ_1P_1$是菱形;当点$Q_2$在$x$轴上方,四边形$ABP_2Q_2$为菱形时,$AQ_2=AB=3\sqrt{2}$,
∴$Q_2(-3,3\sqrt{2})$.同理,可得当四边形$ABP_3Q_3$为菱形时,$Q_3(-3,-3\sqrt{2})$.②当$AB$是菱形的对角线时,设$P_4(0,s),Q_4(m,n)$,
∴$AB$的中点即为$P_4Q_4$的中点,且$P_4A=P_4B$(即$P_4A^2=P_4B^2$).
∴$0+m=-3+0$,$s+n=3$,$(-3-0)^2+s^2=(3-s)^2$.
∴$m=-3$,$n=3$,$s=0$.
∴$Q_4(-3,3)$.综上所述,点$Q$的坐标为$(-3,3\sqrt{2})$或$(-3,-3\sqrt{2})$或$(-3,3)$或$(3,0)$
1.(1)设直线AB对应的函数解析式为$y=kx+b$.将$A(-3,0),C(-2,1)$代入,得$\begin{cases}0=-3k+b,\\1=-2k+b.\end{cases}$解得$\begin{cases}k=1,\\b=3.\end{cases}$
∴直线AB对应的函数解析式为$y=x+3$
(2)存在.
∵直线AB对应的函数解析式为$y=x+3$,
∴令$x=0$,则$y=3$.
∴$B(0,3)$,即$OB=3$.
∵$C(-2,1)$,
∴$S_{\triangle OBC}=\frac{1}{2}OB·|-2|=\frac{1}{2}×3×2=3$.
∴$S_{\triangle OMB}=\frac{3}{2}$.设$M(a,a+3)$.
∴$S_{\triangle OMB}=\frac{1}{2}OB·|a|=\frac{1}{2}×3×|a|=\frac{3}{2}|a|=\frac{3}{2}$,解得$a=-1$或$a=1$.
∴$M(1,4)$或$(-1,2)$
(3)存在.
∵$A(-3,0),B(0,3)$,
∴$AB=\sqrt{3^2+3^2}=3\sqrt{2}$.如图.①当$AB$是菱形的一条边时,点$P_1$与点$B$关于$x$轴对称时,$Q_1(3,0)$是点$A$关于$y$轴的对称点,四边形$ABQ_1P_1$是菱形;当点$Q_2$在$x$轴上方,四边形$ABP_2Q_2$为菱形时,$AQ_2=AB=3\sqrt{2}$,
∴$Q_2(-3,3\sqrt{2})$.同理,可得当四边形$ABP_3Q_3$为菱形时,$Q_3(-3,-3\sqrt{2})$.②当$AB$是菱形的对角线时,设$P_4(0,s),Q_4(m,n)$,
∴$AB$的中点即为$P_4Q_4$的中点,且$P_4A=P_4B$(即$P_4A^2=P_4B^2$).
∴$0+m=-3+0$,$s+n=3$,$(-3-0)^2+s^2=(3-s)^2$.
∴$m=-3$,$n=3$,$s=0$.
∴$Q_4(-3,3)$.综上所述,点$Q$的坐标为$(-3,3\sqrt{2})$或$(-3,-3\sqrt{2})$或$(-3,3)$或$(3,0)$

2. 如图,直线 $ y = 2x - 2 $ 与 $ x $ 轴交于点 $ A $,与 $ y $ 轴交于点 $ B $.
(1) 点 $ A $ 的坐标为
(2) 已知 $ C $ 是直线 $ AB $ 上不同于点 $ B $ 的点,且 $ AC = AB $.
① 求点 $ C $ 的坐标.
② 过动点 $ P(m,0) $ 且垂直于 $ x $ 轴的直线与直线 $ AB $ 交于点 $ E $. 若点 $ E $ 不在线段 $ BC $ 上,则 $ m $ 的取值范围是
(3) 若 $ \angle ABN = 45^{\circ} $,求直线 $ BN $ 对应的函数解析式.
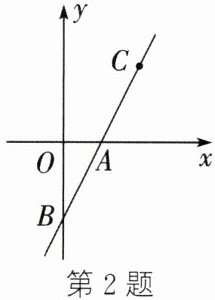
(1) 点 $ A $ 的坐标为
(1,0)
,点 $ B $ 的坐标为 (0,-2)
.(2) 已知 $ C $ 是直线 $ AB $ 上不同于点 $ B $ 的点,且 $ AC = AB $.
① 求点 $ C $ 的坐标.
② 过动点 $ P(m,0) $ 且垂直于 $ x $ 轴的直线与直线 $ AB $ 交于点 $ E $. 若点 $ E $ 不在线段 $ BC $ 上,则 $ m $ 的取值范围是
$m<0$或$m>2$
.(3) 若 $ \angle ABN = 45^{\circ} $,求直线 $ BN $ 对应的函数解析式.

答案:
2.(1)$(1,0)$,$(0,-2)$
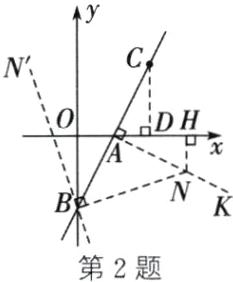
(2)①如图,过点$C$作$CD⊥ x$轴,垂足为$D$,则$\angle ADC=90°$.在$\triangle ABO$和$\triangle ACD$中,
∵$\angle AOB=\angle ADC=90°$,$\angle BAO=\angle CAD$,$AB=AC$,
∴$\triangle ABO\cong\triangle ACD$.
∴$BO=CD$,$AO=AD$.由(1),易得$OA=1$,$OB=2$,
∴$OD=2$,$CD=2$.
∴点$C$的坐标为$(2,2)$
②$m<0$或$m>2$
(3)如图,过点$A$向右下作$AK⊥ AB$,在$AK$上截取$AN=AB$,过点$N$作$NH⊥ x$轴于点$H$,连接$BN$,则$\triangle ABN$是等腰直角三角形,$\angle ABN=45°$.
∴$\angle AOB=\angle BAN=\angle NHA=90°$.
∴$\angle OAB+\angle ABO=90°$,$\angle OAB+\angle NAH=90°$.
∴$\angle ABO=\angle NAH$.在$\triangle ABO$和$\triangle NAH$中,
∵$\angle AOB=\angle NHA$,$\angle ABO=\angle NAH$,$AB=NA$,
∴$\triangle ABO\cong\triangle NAH$.
∴$BO=AH=2$,$AO=NH=1$.
∴$OH=OA+AH=3$.
∴点$N$的坐标为$(3,-1)$.设直线$BN$对应的函数解析式为$y=kx+b$,则$\begin{cases}3k+b=-1,\\b=-2,\end{cases}$解得$\begin{cases}k=\frac{1}{3},\\b=-2.\end{cases}$
∴直线$BN$对应的函数解析式为$y=\frac{1}{3}x-2$.过点$B$作$BN'⊥ BN$,易得直线$BN'$也满足条件.易求得直线$BN'$对应的函数解析式为$y=-3x-2$.综上所述,满足条件的直线$BN$对应的函数解析式为$y=\frac{1}{3}x-2$或$y=-3x-2$
2.(1)$(1,0)$,$(0,-2)$
(2)①如图,过点$C$作$CD⊥ x$轴,垂足为$D$,则$\angle ADC=90°$.在$\triangle ABO$和$\triangle ACD$中,
∵$\angle AOB=\angle ADC=90°$,$\angle BAO=\angle CAD$,$AB=AC$,
∴$\triangle ABO\cong\triangle ACD$.
∴$BO=CD$,$AO=AD$.由(1),易得$OA=1$,$OB=2$,
∴$OD=2$,$CD=2$.
∴点$C$的坐标为$(2,2)$
②$m<0$或$m>2$
(3)如图,过点$A$向右下作$AK⊥ AB$,在$AK$上截取$AN=AB$,过点$N$作$NH⊥ x$轴于点$H$,连接$BN$,则$\triangle ABN$是等腰直角三角形,$\angle ABN=45°$.
∴$\angle AOB=\angle BAN=\angle NHA=90°$.
∴$\angle OAB+\angle ABO=90°$,$\angle OAB+\angle NAH=90°$.
∴$\angle ABO=\angle NAH$.在$\triangle ABO$和$\triangle NAH$中,
∵$\angle AOB=\angle NHA$,$\angle ABO=\angle NAH$,$AB=NA$,
∴$\triangle ABO\cong\triangle NAH$.
∴$BO=AH=2$,$AO=NH=1$.
∴$OH=OA+AH=3$.
∴点$N$的坐标为$(3,-1)$.设直线$BN$对应的函数解析式为$y=kx+b$,则$\begin{cases}3k+b=-1,\\b=-2,\end{cases}$解得$\begin{cases}k=\frac{1}{3},\\b=-2.\end{cases}$
∴直线$BN$对应的函数解析式为$y=\frac{1}{3}x-2$.过点$B$作$BN'⊥ BN$,易得直线$BN'$也满足条件.易求得直线$BN'$对应的函数解析式为$y=-3x-2$.综上所述,满足条件的直线$BN$对应的函数解析式为$y=\frac{1}{3}x-2$或$y=-3x-2$
