13. 已知函数 $ y = 3x + 1 $.
(1) 试判断点 $ A(-1,2) $ 和点 $ B(\frac{1}{3},2) $ 是否在此函数的图象上;
(2) 已知点$ (-a,a - 1) $在此函数图象上,求 $ a $ 的值.
(1) 试判断点 $ A(-1,2) $ 和点 $ B(\frac{1}{3},2) $ 是否在此函数的图象上;
(2) 已知点$ (-a,a - 1) $在此函数图象上,求 $ a $ 的值.
答案:13.(1)把$x = -1$代入$y = 3x + 1$,得$y = 3×(-1) + 1 = -2 \neq 2$,$\therefore$点$A$不在此函数的图象上。把$x = \frac{1}{3}$代入$y = 3x + 1$,得$y = 3×\frac{1}{3} + 1 = 2$,$\therefore$点$B$在此函数的图象上。(2)把$(-a,a - 1)$代入$y = 3x + 1$,得$a - 1 = -3a + 1$,解得$a = \frac{1}{2}$
14. 如图①,在 $ \mathrm{Rt} \triangle ABC $ 中,$ \angle ABC = 90^{\circ} $,$ AB = 3 $,$ BC = 4 $,动点 $ P $ 从点 $ A $ 出发,沿 $ A \to B \to C $ 方向运动,速度为每秒 1 个单位长度,到达点 $ C $ 时停止运动.设点 $ P $ 的运动时间为 $ x $ 秒,$ \triangle ACP $ 的面积为 $ y $.
(1) 写出 $ y $ 关于 $ x $ 的函数解析式,并注明自变量 $ x $ 的取值范围;
(2) 在如图②所示的平面直角坐标系中,画出 $ y $ 的函数图象,并写出函数 $ y $ 的一条性质;
(3) 结合函数图象,写出 $ \triangle ACP $ 的面积大于 3 时 $ x $ 的取值范围(结果保留一位小数,误差不超过 $ 0.2 $).
 ]
]
(1) 写出 $ y $ 关于 $ x $ 的函数解析式,并注明自变量 $ x $ 的取值范围;
(2) 在如图②所示的平面直角坐标系中,画出 $ y $ 的函数图象,并写出函数 $ y $ 的一条性质;
(3) 结合函数图象,写出 $ \triangle ACP $ 的面积大于 3 时 $ x $ 的取值范围(结果保留一位小数,误差不超过 $ 0.2 $).
 ]
]答案:
14.(1)$S_{\triangle ABC} = \frac{1}{2}AB· BC = \frac{1}{2}×3×4 = 6$。当点$P$在$AB$上时,$AP = x$,则$BP = 3 - x$,$0\leq x\leq3$,$\therefore S_{\triangle PBC} = \frac{1}{2}BP· BC = \frac{1}{2}×(3 - x)×4 = 6 - 2x$。$\therefore S_{\triangle ACP} = S_{\triangle ABC} - S_{\triangle PBC} = 2x$,即$y = 2x(0\leq x\leq3)$。当点$P$在$BC$上时,$BP = x - 3$,$3 < x\leq7$,$\therefore S_{\triangle PBA} = \frac{1}{2}BP· AB = \frac{1}{2}×(x - 3)×3 = \frac{3}{2}x - \frac{9}{2}$。$\therefore S_{\triangle ACP} = S_{\triangle ABC} - S_{\triangle PBA} = -\frac{3}{2}x + \frac{21}{2}$,即$y = -\frac{3}{2}x + \frac{21}{2}(3 < x\leq7)$。综上所述,$y = \begin{cases}2x(0\leq x\leq3)\\ -\frac{3}{2}x + \frac{21}{2}(3 < x\leq7)\end{cases}$
(2)函数图象如图所示。当$0\leq x\leq3$时,$y$随$x$的增大而增大;当$3 < x\leq7$时,$y$随$x$的增大而减小(答案不唯一)。(3)当$y = 3$时,$3 = 2x$,解得$x = 1.5$。当$y = 3$时,$3 = -\frac{3}{2}x + \frac{21}{2}$,解得$x = 5$。由图可知,当$1.5 < x < 5$时,$\triangle ACP$的面积大于$3$。
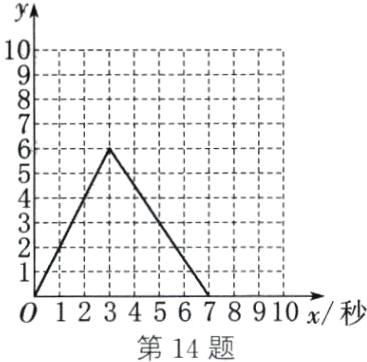
14.(1)$S_{\triangle ABC} = \frac{1}{2}AB· BC = \frac{1}{2}×3×4 = 6$。当点$P$在$AB$上时,$AP = x$,则$BP = 3 - x$,$0\leq x\leq3$,$\therefore S_{\triangle PBC} = \frac{1}{2}BP· BC = \frac{1}{2}×(3 - x)×4 = 6 - 2x$。$\therefore S_{\triangle ACP} = S_{\triangle ABC} - S_{\triangle PBC} = 2x$,即$y = 2x(0\leq x\leq3)$。当点$P$在$BC$上时,$BP = x - 3$,$3 < x\leq7$,$\therefore S_{\triangle PBA} = \frac{1}{2}BP· AB = \frac{1}{2}×(x - 3)×3 = \frac{3}{2}x - \frac{9}{2}$。$\therefore S_{\triangle ACP} = S_{\triangle ABC} - S_{\triangle PBA} = -\frac{3}{2}x + \frac{21}{2}$,即$y = -\frac{3}{2}x + \frac{21}{2}(3 < x\leq7)$。综上所述,$y = \begin{cases}2x(0\leq x\leq3)\\ -\frac{3}{2}x + \frac{21}{2}(3 < x\leq7)\end{cases}$
(2)函数图象如图所示。当$0\leq x\leq3$时,$y$随$x$的增大而增大;当$3 < x\leq7$时,$y$随$x$的增大而减小(答案不唯一)。(3)当$y = 3$时,$3 = 2x$,解得$x = 1.5$。当$y = 3$时,$3 = -\frac{3}{2}x + \frac{21}{2}$,解得$x = 5$。由图可知,当$1.5 < x < 5$时,$\triangle ACP$的面积大于$3$。
