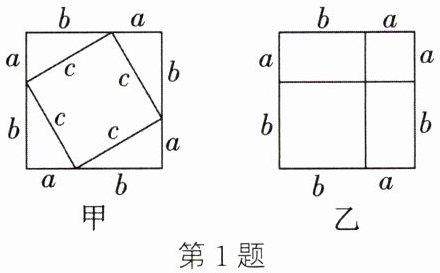
1. 如图,学习勾股定理时,甲同学用四个相同的直角三角形(直角边长分别为$a$,$b$,斜边长为$c$)构成一个大正方形,乙同学用边长分别为$a$,$b$的两个正方形和长为$b$、宽为$a$的两个长方形构成一个大正方形。甲、乙两名同学给出的构图方案,可证明勾股定理的是(
A.甲
B.乙
C.甲、乙都可以
D.甲、乙都不可以
A
)
A.甲
B.乙
C.甲、乙都可以
D.甲、乙都不可以
答案:1.A
解析:
甲图证明:
大正方形边长为 $a+b$,面积为 $(a+b)^2$。
大正方形由4个直角三角形和1个小正方形组成,小正方形边长为 $b-a$(假设 $b>a$),面积为 $(b-a)^2$。
4个直角三角形面积总和为 $4 × \frac{1}{2}ab = 2ab$。
因此:
$(a+b)^2 = 2ab + (b-a)^2$
展开得:
$a^2 + 2ab + b^2 = 2ab + b^2 - 2ab + a^2$
化简后:
$a^2 + b^2 = c^2$
乙图证明:
大正方形边长为 $a+b$,面积为 $(a+b)^2$。
大正方形由边长为 $a$、$b$ 的两个小正方形和2个长方形(面积均为 $ab$)组成。
面积关系为:
$(a+b)^2 = a^2 + b^2 + 2ab$
展开左边得:
$a^2 + 2ab + b^2 = a^2 + b^2 + 2ab$
等式恒成立,但未涉及斜边 $c$,无法证明勾股定理。
结论:仅甲图可证明勾股定理。
A
大正方形边长为 $a+b$,面积为 $(a+b)^2$。
大正方形由4个直角三角形和1个小正方形组成,小正方形边长为 $b-a$(假设 $b>a$),面积为 $(b-a)^2$。
4个直角三角形面积总和为 $4 × \frac{1}{2}ab = 2ab$。
因此:
$(a+b)^2 = 2ab + (b-a)^2$
展开得:
$a^2 + 2ab + b^2 = 2ab + b^2 - 2ab + a^2$
化简后:
$a^2 + b^2 = c^2$
乙图证明:
大正方形边长为 $a+b$,面积为 $(a+b)^2$。
大正方形由边长为 $a$、$b$ 的两个小正方形和2个长方形(面积均为 $ab$)组成。
面积关系为:
$(a+b)^2 = a^2 + b^2 + 2ab$
展开左边得:
$a^2 + 2ab + b^2 = a^2 + b^2 + 2ab$
等式恒成立,但未涉及斜边 $c$,无法证明勾股定理。
结论:仅甲图可证明勾股定理。
A
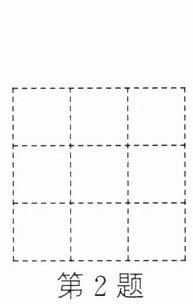
2. 如图,在$3×3$的正方形网格中,若小正方形的边长是$1$,则任意两个格点间的距离不可能是(
A.$\sqrt{7}$
B.$2\sqrt{2}$
C.$3$
D.$\sqrt{10}$
A
)
A.$\sqrt{7}$
B.$2\sqrt{2}$
C.$3$
D.$\sqrt{10}$
答案:2.A
解析:
在$3×3$网格中,格点间距离为$\sqrt{a^2 + b^2}$($a,b$为整数,$0 \leq a,b \leq 3$)。
选项A:$\sqrt{7}$,不存在整数$a,b$使$a^2 + b^2 = 7$。
选项B:$2\sqrt{2} = \sqrt{8}$,$a=2,b=2$时,$2^2 + 2^2 = 8$。
选项C:$3 = \sqrt{9}$,$a=3,b=0$时,$3^2 + 0^2 = 9$。
选项D:$\sqrt{10}$,$a=1,b=3$时,$1^2 + 3^2 = 10$。
A
选项A:$\sqrt{7}$,不存在整数$a,b$使$a^2 + b^2 = 7$。
选项B:$2\sqrt{2} = \sqrt{8}$,$a=2,b=2$时,$2^2 + 2^2 = 8$。
选项C:$3 = \sqrt{9}$,$a=3,b=0$时,$3^2 + 0^2 = 9$。
选项D:$\sqrt{10}$,$a=1,b=3$时,$1^2 + 3^2 = 10$。
A
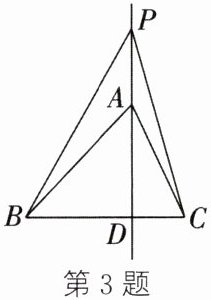
3. 如图,在$\triangle ABC$中,$AB = 10$,$AC = 8$,在高线$AD$所在的直线上任取一点$P$(不与点$A$,$D$重合),连接$PB$,$PC$,则$PB^{2}-PC^{2}$的值为(
A.$6$
B.$18$
C.$36$
D.$72$
C
)
A.$6$
B.$18$
C.$36$
D.$72$
答案:3.C
解析:
证明:
∵ $AD$ 是 $\triangle ABC$ 的高线,
∴ $\angle ADB = \angle ADC = 90°$。
在 $\mathrm{Rt}\triangle ABD$ 和 $\mathrm{Rt}\triangle ACD$ 中,由勾股定理得:
$AB^2 = AD^2 + BD^2$,$AC^2 = AD^2 + CD^2$。
两式相减:$AB^2 - AC^2 = BD^2 - CD^2$。
在 $\mathrm{Rt}\triangle PBD$ 和 $\mathrm{Rt}\triangle PCD$ 中,同理:
$PB^2 = PD^2 + BD^2$,$PC^2 = PD^2 + CD^2$。
两式相减:$PB^2 - PC^2 = BD^2 - CD^2$。
∴ $PB^2 - PC^2 = AB^2 - AC^2$。
∵ $AB = 10$,$AC = 8$,
∴ $PB^2 - PC^2 = 10^2 - 8^2 = 100 - 64 = 36$。
答案:C
∵ $AD$ 是 $\triangle ABC$ 的高线,
∴ $\angle ADB = \angle ADC = 90°$。
在 $\mathrm{Rt}\triangle ABD$ 和 $\mathrm{Rt}\triangle ACD$ 中,由勾股定理得:
$AB^2 = AD^2 + BD^2$,$AC^2 = AD^2 + CD^2$。
两式相减:$AB^2 - AC^2 = BD^2 - CD^2$。
在 $\mathrm{Rt}\triangle PBD$ 和 $\mathrm{Rt}\triangle PCD$ 中,同理:
$PB^2 = PD^2 + BD^2$,$PC^2 = PD^2 + CD^2$。
两式相减:$PB^2 - PC^2 = BD^2 - CD^2$。
∴ $PB^2 - PC^2 = AB^2 - AC^2$。
∵ $AB = 10$,$AC = 8$,
∴ $PB^2 - PC^2 = 10^2 - 8^2 = 100 - 64 = 36$。
答案:C
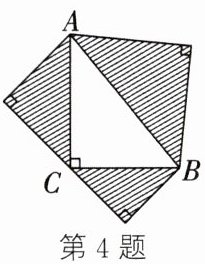
4. 如图,以$Rt\triangle ABC$的三边为斜边分别向外作等腰直角三角形。若斜边$AB = 3$,则图中阴影部分的面积为(
A.$9$
B.$3$
C.$\frac{9}{4}$
D.$\frac{9}{2}$
D
)
A.$9$
B.$3$
C.$\frac{9}{4}$
D.$\frac{9}{2}$
答案:4.D
解析:
设以$AC$为斜边的等腰直角三角形的直角边长为$a$,以$BC$为斜边的等腰直角三角形的直角边长为$b$,以$AB$为斜边的等腰直角三角形的直角边长为$c$。
在等腰直角三角形中,斜边与直角边的关系为:斜边$=\sqrt{2}×$直角边,故直角边$=\frac{\mathrm{斜边}}{\sqrt{2}}$。
其面积为$\frac{1}{2}×$直角边$^{2}=\frac{1}{2}×(\frac{\mathrm{斜边}}{\sqrt{2}})^{2}=\frac{1}{2}×\frac{\mathrm{斜边}^{2}}{2}=\frac{\mathrm{斜边}^{2}}{4}$。
所以以$AC$为斜边的等腰直角三角形面积$S_{1}=\frac{AC^{2}}{4}$,以$BC$为斜边的等腰直角三角形面积$S_{2}=\frac{BC^{2}}{4}$,以$AB$为斜边的等腰直角三角形面积$S_{3}=\frac{AB^{2}}{4}$。
阴影部分面积$S=S_{1}+S_{2}+S_{3}=\frac{AC^{2}+BC^{2}+AB^{2}}{4}$。
在$Rt\triangle ABC$中,由勾股定理得$AC^{2}+BC^{2}=AB^{2}=3^{2}=9$。
则$S=\frac{9 + 9}{4}=\frac{18}{4}=\frac{9}{2}$。
答案:D
在等腰直角三角形中,斜边与直角边的关系为:斜边$=\sqrt{2}×$直角边,故直角边$=\frac{\mathrm{斜边}}{\sqrt{2}}$。
其面积为$\frac{1}{2}×$直角边$^{2}=\frac{1}{2}×(\frac{\mathrm{斜边}}{\sqrt{2}})^{2}=\frac{1}{2}×\frac{\mathrm{斜边}^{2}}{2}=\frac{\mathrm{斜边}^{2}}{4}$。
所以以$AC$为斜边的等腰直角三角形面积$S_{1}=\frac{AC^{2}}{4}$,以$BC$为斜边的等腰直角三角形面积$S_{2}=\frac{BC^{2}}{4}$,以$AB$为斜边的等腰直角三角形面积$S_{3}=\frac{AB^{2}}{4}$。
阴影部分面积$S=S_{1}+S_{2}+S_{3}=\frac{AC^{2}+BC^{2}+AB^{2}}{4}$。
在$Rt\triangle ABC$中,由勾股定理得$AC^{2}+BC^{2}=AB^{2}=3^{2}=9$。
则$S=\frac{9 + 9}{4}=\frac{18}{4}=\frac{9}{2}$。
答案:D
5. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AB = 12$,分别以$AC$,$BC$为直径作半圆,面积分别记为$S_{1}$,$S_{2}$,则$S_{1}+S_{2}$等于
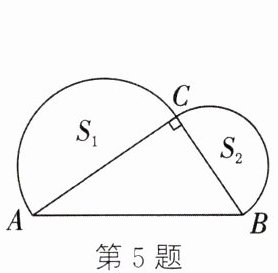
18π
。
答案:5.18π
解析:
解:在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AB = 12$,由勾股定理得$AC^{2}+BC^{2}=AB^{2}=12^{2}=144$。
$S_{1}$为以$AC$为直径的半圆面积,$S_{1}=\frac{1}{2}\pi(\frac{AC}{2})^{2}=\frac{\pi AC^{2}}{8}$;
$S_{2}$为以$BC$为直径的半圆面积,$S_{2}=\frac{1}{2}\pi(\frac{BC}{2})^{2}=\frac{\pi BC^{2}}{8}$。
则$S_{1}+S_{2}=\frac{\pi AC^{2}}{8}+\frac{\pi BC^{2}}{8}=\frac{\pi(AC^{2}+BC^{2})}{8}=\frac{\pi×144}{8}=18\pi$。
18π
$S_{1}$为以$AC$为直径的半圆面积,$S_{1}=\frac{1}{2}\pi(\frac{AC}{2})^{2}=\frac{\pi AC^{2}}{8}$;
$S_{2}$为以$BC$为直径的半圆面积,$S_{2}=\frac{1}{2}\pi(\frac{BC}{2})^{2}=\frac{\pi BC^{2}}{8}$。
则$S_{1}+S_{2}=\frac{\pi AC^{2}}{8}+\frac{\pi BC^{2}}{8}=\frac{\pi(AC^{2}+BC^{2})}{8}=\frac{\pi×144}{8}=18\pi$。
18π
6. 如图,把一块含$45^{\circ}$角的三角板放入网格中,三角板三个顶点均在格点上,直角顶点与数轴上表示$-1$的点重合,则数轴上点$A$所表示的数为
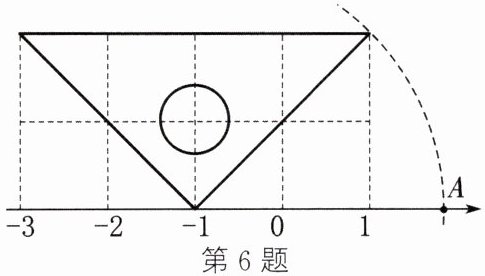
2$\sqrt{2}$−1
。
答案:6.2$\sqrt{2}$−1
解析:
解:由图可知,三角板为等腰直角三角形,直角顶点在数轴上表示$-1$的点,另两个顶点分别在$(-3,2)$和$(1,2)$处。
直角边长度为:$\sqrt{(-3 - (-1))^2 + (2 - 0)^2} = \sqrt{(-2)^2 + 2^2} = \sqrt{4 + 4} = \sqrt{8} = 2\sqrt{2}$
点$A$与直角顶点的距离等于直角边长度$2\sqrt{2}$,且在数轴正方向,所以点$A$表示的数为$-1 + 2\sqrt{2} = 2\sqrt{2} - 1$
$2\sqrt{2} - 1$
直角边长度为:$\sqrt{(-3 - (-1))^2 + (2 - 0)^2} = \sqrt{(-2)^2 + 2^2} = \sqrt{4 + 4} = \sqrt{8} = 2\sqrt{2}$
点$A$与直角顶点的距离等于直角边长度$2\sqrt{2}$,且在数轴正方向,所以点$A$表示的数为$-1 + 2\sqrt{2} = 2\sqrt{2} - 1$
$2\sqrt{2} - 1$
7. 如图,某村庄$A$与公路$l$之间有一池塘,村民出行都走$AB$这条村级公路。在美丽乡村建设过程中,为了便于村民出行,村委会治理了池塘并在村庄$A$到公路$l$之间架桥,新修了一条公路$AC$,且$AC⊥ l$,测得$CB = 2\sqrt{2}$km,$AB = 4\sqrt{2}$km。
(1)求新修的公路$AC$的长;
(2)在后期的建设中,村委会在$B$,$C$两点之间修建了一个观光亭$D$,使得观光亭$D$到点$C$的距离与观光亭$D$到点$B$的距离相等,求观光亭$D$到村庄$A$的距离。
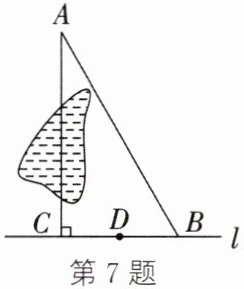
(1)求新修的公路$AC$的长;
(2)在后期的建设中,村委会在$B$,$C$两点之间修建了一个观光亭$D$,使得观光亭$D$到点$C$的距离与观光亭$D$到点$B$的距离相等,求观光亭$D$到村庄$A$的距离。

答案:
7.(1)
∵AC⊥l,
∴∠ACB = 90°.
∴在Rt△ABC中,AC = $\sqrt{AB^{2}-BC^{2}}=\sqrt{(4\sqrt{2})^{2}-(2\sqrt{2})^{2}}=2\sqrt{6}$(km) (2)如图,连接AD.
∵观光亭D到点C的距离与观光亭D到点B的距离相等,
∴D为BC的中点.
∴CD = $\frac{1}{2}$CB = $\frac{1}{2}$×2$\sqrt{2}$ = $\sqrt{2}$(km).
∴在Rt△ACD中,AD = $\sqrt{AC^{2}+CD^{2}}=\sqrt{(2\sqrt{6})^{2}+(\sqrt{2})^{2}}=\sqrt{26}$(km).
∴观光亭D到村庄A的距离为$\sqrt{26}$km
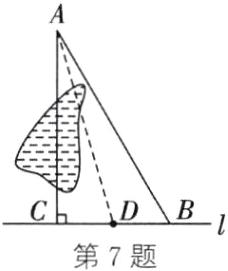
7.(1)
∵AC⊥l,
∴∠ACB = 90°.
∴在Rt△ABC中,AC = $\sqrt{AB^{2}-BC^{2}}=\sqrt{(4\sqrt{2})^{2}-(2\sqrt{2})^{2}}=2\sqrt{6}$(km) (2)如图,连接AD.
∵观光亭D到点C的距离与观光亭D到点B的距离相等,
∴D为BC的中点.
∴CD = $\frac{1}{2}$CB = $\frac{1}{2}$×2$\sqrt{2}$ = $\sqrt{2}$(km).
∴在Rt△ACD中,AD = $\sqrt{AC^{2}+CD^{2}}=\sqrt{(2\sqrt{6})^{2}+(\sqrt{2})^{2}}=\sqrt{26}$(km).
∴观光亭D到村庄A的距离为$\sqrt{26}$km
