12. 使式子$\sqrt{\dfrac{1}{3}x - 2}$有意义的$x$的最小整数值是
6
.答案:12.6
解析:
要使式子$\sqrt{\dfrac{1}{3}x - 2}$有意义,则被开方数必须是非负数,即$\dfrac{1}{3}x - 2 \geq 0$。
解不等式:
$\dfrac{1}{3}x - 2 \geq 0$
$\dfrac{1}{3}x \geq 2$
$x \geq 2 × 3$
$x \geq 6$
所以$x$的最小整数值是$6$。
6
解不等式:
$\dfrac{1}{3}x - 2 \geq 0$
$\dfrac{1}{3}x \geq 2$
$x \geq 2 × 3$
$x \geq 6$
所以$x$的最小整数值是$6$。
6
13. 若$a$,$b$为有理数,且$\sqrt{8} + \sqrt{18} + \sqrt{\dfrac{1}{8}} = a + b\sqrt{2}$,则$ab =$
0
.答案:13.0
解析:
$\sqrt{8} + \sqrt{18} + \sqrt{\dfrac{1}{8}} = 2\sqrt{2} + 3\sqrt{2} + \dfrac{\sqrt{2}}{4} = (2 + 3 + \dfrac{1}{4})\sqrt{2} = \dfrac{21}{4}\sqrt{2}$,所以$a = 0$,$b = \dfrac{21}{4}$,则$ab = 0×\dfrac{21}{4} = 0$。
14. 我国南宋数学家秦九韶曾提出利用三角形的三边长求面积的公式:若一个三角形的三边长分别为$a$,$b$,$c$,则三角形的面积$S = \sqrt{\dfrac{1}{4}[a^{2}b^{2} - (\dfrac{a^{2} + b^{2} - c^{2}}{2})^{2}]}$.若$a = 2\sqrt{2}$,$b = 3$,$c = 1$,则$S$的值为
$\sqrt{2}$
.答案:$14.\sqrt{2}$
解析:
$a=2\sqrt{2}$,$b=3$,$c=1$,
$a^{2}=(2\sqrt{2})^{2}=8$,$b^{2}=3^{2}=9$,$c^{2}=1^{2}=1$,
$a^{2}b^{2}=8×9=72$,
$\dfrac{a^{2}+b^{2}-c^{2}}{2}=\dfrac{8 + 9 - 1}{2}=\dfrac{16}{2}=8$,
$(\dfrac{a^{2}+b^{2}-c^{2}}{2})^{2}=8^{2}=64$,
$\dfrac{1}{4}[a^{2}b^{2}-(\dfrac{a^{2}+b^{2}-c^{2}}{2})^{2}]=\dfrac{1}{4}(72 - 64)=\dfrac{1}{4}×8=2$,
$S=\sqrt{2}$
$a^{2}=(2\sqrt{2})^{2}=8$,$b^{2}=3^{2}=9$,$c^{2}=1^{2}=1$,
$a^{2}b^{2}=8×9=72$,
$\dfrac{a^{2}+b^{2}-c^{2}}{2}=\dfrac{8 + 9 - 1}{2}=\dfrac{16}{2}=8$,
$(\dfrac{a^{2}+b^{2}-c^{2}}{2})^{2}=8^{2}=64$,
$\dfrac{1}{4}[a^{2}b^{2}-(\dfrac{a^{2}+b^{2}-c^{2}}{2})^{2}]=\dfrac{1}{4}(72 - 64)=\dfrac{1}{4}×8=2$,
$S=\sqrt{2}$
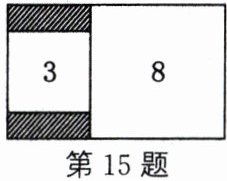
15. 如图,在一个长方形内有两个正方形,面积分别为$8$,$3$,则阴影部分的面积之和为
$2\sqrt{6}-3$
.
答案:$15.2\sqrt{6}-3$
解析:
面积为8的正方形边长为$\sqrt{8}=2\sqrt{2}$,面积为3的正方形边长为$\sqrt{3}$。阴影部分面积之和为$(2\sqrt{2}-\sqrt{3})×\sqrt{3}=2\sqrt{6}-3$。
16. 我们根据二次根式的相关知识容易知道:$\sqrt{2\dfrac{2}{3}} = 2\sqrt{\dfrac{2}{3}}$,$\sqrt{3\dfrac{3}{8}} = 3\sqrt{\dfrac{3}{8}}$,$\sqrt{4\dfrac{4}{15}} = 4\sqrt{\dfrac{4}{15}}$,…,若$\sqrt{9\dfrac{9}{n}} = 9\sqrt{\dfrac{9}{n}}$,则$n =$
80
.答案:16.80
解析:
$\sqrt{9\dfrac{9}{n}} = \sqrt{\dfrac{9n + 9}{n}} = \sqrt{\dfrac{9(n + 1)}{n}}$,$9\sqrt{\dfrac{9}{n}} = 9×\dfrac{3}{\sqrt{n}} = \dfrac{27}{\sqrt{n}}$。
因为$\sqrt{\dfrac{9(n + 1)}{n}} = \dfrac{27}{\sqrt{n}}$,两边平方得$\dfrac{9(n + 1)}{n} = \dfrac{729}{n}$,
两边同乘$n$得$9(n + 1) = 729$,
$n + 1 = 81$,
$n = 80$。
80
因为$\sqrt{\dfrac{9(n + 1)}{n}} = \dfrac{27}{\sqrt{n}}$,两边平方得$\dfrac{9(n + 1)}{n} = \dfrac{729}{n}$,
两边同乘$n$得$9(n + 1) = 729$,
$n + 1 = 81$,
$n = 80$。
80
17. (6分)化简:
(1)$\sqrt{405}$;
(2)$\sqrt{\dfrac{7}{8}}$;
(3)$\sqrt{\dfrac{m^{2}}{25n^{3}}}(m > 0,n > 0)$.
(1)$\sqrt{405}$;
(2)$\sqrt{\dfrac{7}{8}}$;
(3)$\sqrt{\dfrac{m^{2}}{25n^{3}}}(m > 0,n > 0)$.
答案:$17.(1)9\sqrt{5} (2)\frac{\sqrt{14}}{4} (3)\frac{m\sqrt{n}}{5n^{2}}$
解析:
(1)$\sqrt{405}=\sqrt{81×5}=\sqrt{81}×\sqrt{5}=9\sqrt{5}$;
(2)$\sqrt{\dfrac{7}{8}}=\sqrt{\dfrac{7×2}{8×2}}=\sqrt{\dfrac{14}{16}}=\dfrac{\sqrt{14}}{\sqrt{16}}=\dfrac{\sqrt{14}}{4}$;
(3)$\sqrt{\dfrac{m^{2}}{25n^{3}}}=\dfrac{\sqrt{m^{2}}}{\sqrt{25n^{3}}}=\dfrac{m}{5n\sqrt{n}}=\dfrac{m\sqrt{n}}{5n^{2}}$.
(2)$\sqrt{\dfrac{7}{8}}=\sqrt{\dfrac{7×2}{8×2}}=\sqrt{\dfrac{14}{16}}=\dfrac{\sqrt{14}}{\sqrt{16}}=\dfrac{\sqrt{14}}{4}$;
(3)$\sqrt{\dfrac{m^{2}}{25n^{3}}}=\dfrac{\sqrt{m^{2}}}{\sqrt{25n^{3}}}=\dfrac{m}{5n\sqrt{n}}=\dfrac{m\sqrt{n}}{5n^{2}}$.
18. (8分)计算:
(1)$\sqrt{125} - (2\sqrt{27} - 7\sqrt{75} + 4\sqrt{45})$;
(2)$(2\sqrt{6} + \sqrt{\dfrac{2}{3}})× \sqrt{3} - \sqrt{32}$;
(3)$(2\sqrt{3} - 5\sqrt{2})(\sqrt{3} - 2\sqrt{2})$;
(4)$(\sqrt{3} + 1)^{2} - 6\sqrt{\dfrac{1}{3}} - (2\sqrt{2} + 1)(2\sqrt{2} - 1)$.
(1)$\sqrt{125} - (2\sqrt{27} - 7\sqrt{75} + 4\sqrt{45})$;
(2)$(2\sqrt{6} + \sqrt{\dfrac{2}{3}})× \sqrt{3} - \sqrt{32}$;
(3)$(2\sqrt{3} - 5\sqrt{2})(\sqrt{3} - 2\sqrt{2})$;
(4)$(\sqrt{3} + 1)^{2} - 6\sqrt{\dfrac{1}{3}} - (2\sqrt{2} + 1)(2\sqrt{2} - 1)$.
答案:$18.(1)29\sqrt{3}-7\sqrt{5} (2)3\sqrt{2} (3)26-9\sqrt{6} (4)-3$
解析:
(1)$\sqrt{125} - (2\sqrt{27} - 7\sqrt{75} + 4\sqrt{45})$
$=5\sqrt{5}-(2× 3\sqrt{3}-7× 5\sqrt{3}+4× 3\sqrt{5})$
$=5\sqrt{5}-(6\sqrt{3}-35\sqrt{3}+12\sqrt{5})$
$=5\sqrt{5}-(-29\sqrt{3}+12\sqrt{5})$
$=5\sqrt{5}+29\sqrt{3}-12\sqrt{5}$
$=29\sqrt{3}-7\sqrt{5}$
(2)$(2\sqrt{6} + \sqrt{\dfrac{2}{3}})× \sqrt{3} - \sqrt{32}$
$=2\sqrt{6}× \sqrt{3}+\sqrt{\dfrac{2}{3}}× \sqrt{3}-4\sqrt{2}$
$=2\sqrt{18}+\sqrt{2}-4\sqrt{2}$
$=2× 3\sqrt{2}+\sqrt{2}-4\sqrt{2}$
$=6\sqrt{2}+\sqrt{2}-4\sqrt{2}$
$=3\sqrt{2}$
(3)$(2\sqrt{3} - 5\sqrt{2})(\sqrt{3} - 2\sqrt{2})$
$=2\sqrt{3}× \sqrt{3}-2\sqrt{3}× 2\sqrt{2}-5\sqrt{2}× \sqrt{3}+5\sqrt{2}× 2\sqrt{2}$
$=6 - 4\sqrt{6}-5\sqrt{6}+20$
$=26 - 9\sqrt{6}$
(4)$(\sqrt{3} + 1)^{2} - 6\sqrt{\dfrac{1}{3}} - (2\sqrt{2} + 1)(2\sqrt{2} - 1)$
$=3 + 2\sqrt{3}+1 - 6× \dfrac{\sqrt{3}}{3}-[(2\sqrt{2})^{2}-1^{2}]$
$=4 + 2\sqrt{3}-2\sqrt{3}-(8 - 1)$
$=4 - 7$
$=-3$
$=5\sqrt{5}-(2× 3\sqrt{3}-7× 5\sqrt{3}+4× 3\sqrt{5})$
$=5\sqrt{5}-(6\sqrt{3}-35\sqrt{3}+12\sqrt{5})$
$=5\sqrt{5}-(-29\sqrt{3}+12\sqrt{5})$
$=5\sqrt{5}+29\sqrt{3}-12\sqrt{5}$
$=29\sqrt{3}-7\sqrt{5}$
(2)$(2\sqrt{6} + \sqrt{\dfrac{2}{3}})× \sqrt{3} - \sqrt{32}$
$=2\sqrt{6}× \sqrt{3}+\sqrt{\dfrac{2}{3}}× \sqrt{3}-4\sqrt{2}$
$=2\sqrt{18}+\sqrt{2}-4\sqrt{2}$
$=2× 3\sqrt{2}+\sqrt{2}-4\sqrt{2}$
$=6\sqrt{2}+\sqrt{2}-4\sqrt{2}$
$=3\sqrt{2}$
(3)$(2\sqrt{3} - 5\sqrt{2})(\sqrt{3} - 2\sqrt{2})$
$=2\sqrt{3}× \sqrt{3}-2\sqrt{3}× 2\sqrt{2}-5\sqrt{2}× \sqrt{3}+5\sqrt{2}× 2\sqrt{2}$
$=6 - 4\sqrt{6}-5\sqrt{6}+20$
$=26 - 9\sqrt{6}$
(4)$(\sqrt{3} + 1)^{2} - 6\sqrt{\dfrac{1}{3}} - (2\sqrt{2} + 1)(2\sqrt{2} - 1)$
$=3 + 2\sqrt{3}+1 - 6× \dfrac{\sqrt{3}}{3}-[(2\sqrt{2})^{2}-1^{2}]$
$=4 + 2\sqrt{3}-2\sqrt{3}-(8 - 1)$
$=4 - 7$
$=-3$