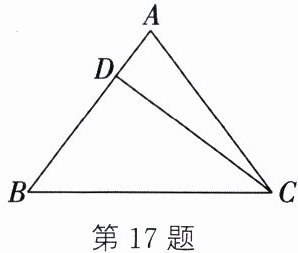
17. (6 分)如图,在△ABC 中,AB = AC,BC = 20 cm,D 是 AB 上一点,且 CD = 16 cm,BD = 12 cm.
(1)CD 与 AB 有何位置关系?请说明理由.
(2)求 AD 的长.
(1)CD 与 AB 有何位置关系?请说明理由.
(2)求 AD 的长.

答案:17.(1)$CD⊥AB$ 理由:
∵$BD = 12cm$,$CD = 16cm$,$BC = 20cm$,
∴易得$BD^{2}+CD^{2}=BC^{2}$.
∴$△BCD$是直角三角形,且$∠BDC = 90°$.
∴$CD⊥AB$. (2)设$AD = xcm(x>0)$,则$AC = AB=(x + 12)cm$.
∵$CD⊥AB$,
∴$∠ADC = 90°$.在$Rt△ADC$中,由勾股定理,得$AD^{2}+CD^{2}=AC^{2}$,即$x^{2}+16^{2}=(x + 12)^{2}$,解得$x=\frac{14}{3}$.
∴$AD$的长为$\frac{14}{3}cm$
∵$BD = 12cm$,$CD = 16cm$,$BC = 20cm$,
∴易得$BD^{2}+CD^{2}=BC^{2}$.
∴$△BCD$是直角三角形,且$∠BDC = 90°$.
∴$CD⊥AB$. (2)设$AD = xcm(x>0)$,则$AC = AB=(x + 12)cm$.
∵$CD⊥AB$,
∴$∠ADC = 90°$.在$Rt△ADC$中,由勾股定理,得$AD^{2}+CD^{2}=AC^{2}$,即$x^{2}+16^{2}=(x + 12)^{2}$,解得$x=\frac{14}{3}$.
∴$AD$的长为$\frac{14}{3}cm$
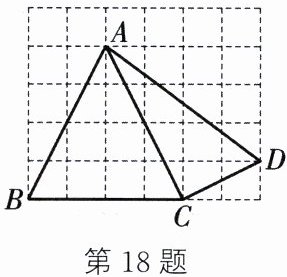
18. (8 分)如图,在由边长为 1 的小正方形组成的网格中,四边形 ABCD 的顶点均在格点上.
(1)求证:△ACD 是直角三角形;
(2)求四边形 ABCD 的面积.
(1)求证:△ACD 是直角三角形;
(2)求四边形 ABCD 的面积.

答案:18.(1)根据题意,得$AC = \sqrt{4^{2}+2^{2}} = 2\sqrt{5}$,$CD = \sqrt{2^{2}+1^{2}}=\sqrt{5}$,$AD = \sqrt{3^{2}+4^{2}} = 5$.
∵$AC^{2}+CD^{2}=(2\sqrt{5})^{2}+(\sqrt{5})^{2}=25=5^{2}=AD^{2}$,
∴$△ACD$是直角三角形 (2)$S_{四边形ABCD}=S_{△ABC}+S_{△ACD}=\frac{1}{2}×4×4+\frac{1}{2}×\sqrt{5}×2\sqrt{5}=8 + 5 = 13$
∵$AC^{2}+CD^{2}=(2\sqrt{5})^{2}+(\sqrt{5})^{2}=25=5^{2}=AD^{2}$,
∴$△ACD$是直角三角形 (2)$S_{四边形ABCD}=S_{△ABC}+S_{△ACD}=\frac{1}{2}×4×4+\frac{1}{2}×\sqrt{5}×2\sqrt{5}=8 + 5 = 13$
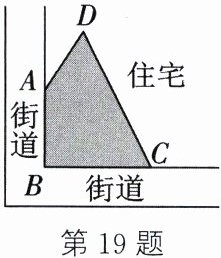
19. (8 分)某小区在社区管理人员及社区居民的共同努力之下,在街道的拐角处建造了一块绿化地(涂色部分). 如图,AB = 9 m,BC = 12 m,CD = 17 m,AD = 8 m,技术人员通过测量确定了∠ABC = 90°.
(1)小区内部分居民每天必须从点 A 经过点 B 再到点 C 的位置,为了方便居民出入,技术人员打算在绿地中开辟一条从点 A 直通点 C 的小路. 请问如果方案落实且施工完成,那么居民从点 A 到点 C 将少走多少米?
(2)这块绿化地的面积是多少?
(1)小区内部分居民每天必须从点 A 经过点 B 再到点 C 的位置,为了方便居民出入,技术人员打算在绿地中开辟一条从点 A 直通点 C 的小路. 请问如果方案落实且施工完成,那么居民从点 A 到点 C 将少走多少米?
(2)这块绿化地的面积是多少?

答案:19.(1)连接$AC$.
∵$∠ABC = 90°$,$AB = 9m$,$BC = 12m$,
∴在$Rt△ABC$中,由勾股定理,得$AC = \sqrt{AB^{2}+BC^{2}}=\sqrt{9^{2}+12^{2}} = 15(m)$.
∴$AB + BC - AC = 9 + 12 - 15 = 6(m)$.
∴居民从点$A$到点$C$将少走$6m$ (2)
∵$CD = 17m$,$AD = 8m$,$AC = 15m$,
∴$AD^{2}+AC^{2}=CD^{2}$.
∴$△DAC$是直角三角形,且$∠DAC = 90°$.
∴$S_{△DAC}=\frac{1}{2}AD· AC=\frac{1}{2}×8×15=60(m^{2})$.又
∵$S_{△ABC}=\frac{1}{2}AB· BC=\frac{1}{2}×9×12 = 54(m^{2})$,
∴$S_{四边形ABCD}=S_{△DAC}+S_{△ABC}=60 + 54 = 114(m^{2})$.
∴这块绿化地的面积是$114m^{2}$
∵$∠ABC = 90°$,$AB = 9m$,$BC = 12m$,
∴在$Rt△ABC$中,由勾股定理,得$AC = \sqrt{AB^{2}+BC^{2}}=\sqrt{9^{2}+12^{2}} = 15(m)$.
∴$AB + BC - AC = 9 + 12 - 15 = 6(m)$.
∴居民从点$A$到点$C$将少走$6m$ (2)
∵$CD = 17m$,$AD = 8m$,$AC = 15m$,
∴$AD^{2}+AC^{2}=CD^{2}$.
∴$△DAC$是直角三角形,且$∠DAC = 90°$.
∴$S_{△DAC}=\frac{1}{2}AD· AC=\frac{1}{2}×8×15=60(m^{2})$.又
∵$S_{△ABC}=\frac{1}{2}AB· BC=\frac{1}{2}×9×12 = 54(m^{2})$,
∴$S_{四边形ABCD}=S_{△DAC}+S_{△ABC}=60 + 54 = 114(m^{2})$.
∴这块绿化地的面积是$114m^{2}$