1. (1)(
(2)在 6:7,0.7:$\frac{3}{5}$,$\frac{2}{21}$:$\frac{4}{21}$三个比中,能与$\frac{2}{3}$:$\frac{4}{7}$组成比例的一个比是(
6
):16 = 3:8 = $\frac{27}{(\ \ \ \ )}$ = 15 ÷(40
)=(0.375
)(最后一空填小数)(2)在 6:7,0.7:$\frac{3}{5}$,$\frac{2}{21}$:$\frac{4}{21}$三个比中,能与$\frac{2}{3}$:$\frac{4}{7}$组成比例的一个比是(
0.7:$\frac{3}{5}$
),组成的比例的内项积是(0.4
)。答案:1. (1) 6 72 40 0.375 (2) 0.7:$\frac{3}{5}$ 0.4
解析:
(1)6;72;40;0.375
(2)0.7:$\frac{3}{5}$;0.4
(2)0.7:$\frac{3}{5}$;0.4
2. 解比例。
$x:\frac{3}{4}=\frac{5}{6}:10$ $0.25:x = 1.6:2.4$
$x:\frac{3}{4}=\frac{5}{6}:10$ $0.25:x = 1.6:2.4$
答案:2. x=$\frac{1}{16}$ x=$\frac{3}{8}$
解析:
解:$x:\frac{3}{4}=\frac{5}{6}:10$
$10x=\frac{3}{4}×\frac{5}{6}$
$10x=\frac{15}{24}$
$10x=\frac{5}{8}$
$x=\frac{5}{8}÷10$
$x=\frac{5}{8}×\frac{1}{10}$
$x=\frac{1}{16}$
解:$0.25:x = 1.6:2.4$
$1.6x=0.25×2.4$
$1.6x=0.6$
$x=0.6÷1.6$
$x=\frac{6}{10}×\frac{10}{16}$
$x=\frac{6}{16}$
$x=\frac{3}{8}$
$10x=\frac{3}{4}×\frac{5}{6}$
$10x=\frac{15}{24}$
$10x=\frac{5}{8}$
$x=\frac{5}{8}÷10$
$x=\frac{5}{8}×\frac{1}{10}$
$x=\frac{1}{16}$
解:$0.25:x = 1.6:2.4$
$1.6x=0.25×2.4$
$1.6x=0.6$
$x=0.6÷1.6$
$x=\frac{6}{10}×\frac{10}{16}$
$x=\frac{6}{16}$
$x=\frac{3}{8}$
3. (2025·苏州吴江区期末)中华人民共和国国旗的旗面是长方形,其长和宽的比是 3:2,某种通用尺度的国旗的周长是 320 厘米,这种尺度的国旗的宽是多少厘米?
答案:3. 320÷2×$\frac{2}{3+2}$=64(厘米)
4. 在比例尺是 1:5000000 的地图上量得甲、乙两地间的距离是 9.6 厘米,一辆客车和一辆货车分别从甲、乙两地同时出发,相向而行,经过 4 小时相遇。已知客车与货车的速度比是 3:2,客车和货车的速度分别是多少?
答案:4. 9.6×5000000=48000000(厘米) 48000000厘米=480千米 480÷4=120(千米/时)
客车:120×$\frac{3}{3+2}$=72(千米/时)
货车:120×$\frac{2}{3+2}$=48(千米/时)
客车:120×$\frac{3}{3+2}$=72(千米/时)
货车:120×$\frac{2}{3+2}$=48(千米/时)
5. 新素养 几何直观 如图,平行四边形被分成甲、乙、丙 3 个三角形,乙与丙的面积之比是 4:5,那么甲与丙的面积之比为(
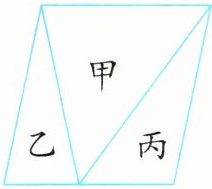
9:5
);甲的面积比丙多 24 平方厘米,这个平行四边形的面积是(108
)平方厘米。
答案:5. 9:5 108
解析:
9:5;108
6. 已知水果店运来苹果、梨和橘子共 580 箱,其中苹果与梨箱数的比是 5:2,橘子与苹果箱数的比是 3:2,则运来苹果、梨、橘子各多少箱?
答案:6. 苹果、梨、橘子的箱数比是10:4:15。
苹果:580÷(10+4+15)×10=200(箱)
梨:580÷(10+4+15)×4=80(箱)
橘子:580÷(10+4+15)×15=300(箱)
苹果:580÷(10+4+15)×10=200(箱)
梨:580÷(10+4+15)×4=80(箱)
橘子:580÷(10+4+15)×15=300(箱)
7. 亮点原创·小红、小华和小明都是集邮爱好者,小红的邮票枚数与其他两人邮票总枚数的比是 5:19,若小华送给小红 12 枚邮票,则他们三人的邮票枚数一样多。他们一共集了(
96
)枚邮票。答案:7. 96 解析 原来小红的邮票枚数占三人邮票总枚数的$\frac{5}{5+19}$,后来占三人邮票总枚数的$\frac{1}{3}$,三人邮票总枚数不变,小红多了小华送给她的12枚邮票,对应邮票总枚数的($\frac{1}{3}-\frac{5}{5+19}$),则三人邮票总枚数为12÷($\frac{1}{3}-\frac{5}{5+19}$)=96(枚)。
解析:
原来小红的邮票枚数占三人邮票总枚数的$\frac{5}{5+19}=\frac{5}{24}$,后来三人邮票枚数一样多,此时小红的邮票枚数占总枚数的$\frac{1}{3}$。
小红多的12枚邮票对应总枚数的$\frac{1}{3}-\frac{5}{24}=\frac{8}{24}-\frac{5}{24}=\frac{3}{24}=\frac{1}{8}$。
则三人邮票总枚数为$12÷\frac{1}{8}=96$枚。
96
小红多的12枚邮票对应总枚数的$\frac{1}{3}-\frac{5}{24}=\frac{8}{24}-\frac{5}{24}=\frac{3}{24}=\frac{1}{8}$。
则三人邮票总枚数为$12÷\frac{1}{8}=96$枚。
96
8. 把 420 毫升油倒入甲、乙两个壶中,如果先把甲壶装满,乙壶只能装 75%;如果先把乙壶装满,甲壶只能装一半。甲、乙两壶各可装油多少毫升?
答案:8. 乙壶的$\frac{1}{4}$=甲壶的$\frac{1}{2}$,则甲壶容积:乙壶容积=1:2 甲壶:420÷(2+$\frac{1}{2}$)=168(毫升)
乙壶:168×2=336(毫升) 解析 油的总量不变,甲、乙两壶的总容积也不变,所以装完油后,两壶空余的容积也相等,即乙壶的(1—75%)等于甲壶的(1—50%),所以甲壶和乙壶容积的比是1:2。420毫升油能把乙壶装满,甲壶装一半,则甲壶的容积是420÷(2+$\frac{1}{2}$)=168(毫升),乙壶的容积则为168×2=336(毫升)。
乙壶:168×2=336(毫升) 解析 油的总量不变,甲、乙两壶的总容积也不变,所以装完油后,两壶空余的容积也相等,即乙壶的(1—75%)等于甲壶的(1—50%),所以甲壶和乙壶容积的比是1:2。420毫升油能把乙壶装满,甲壶装一半,则甲壶的容积是420÷(2+$\frac{1}{2}$)=168(毫升),乙壶的容积则为168×2=336(毫升)。