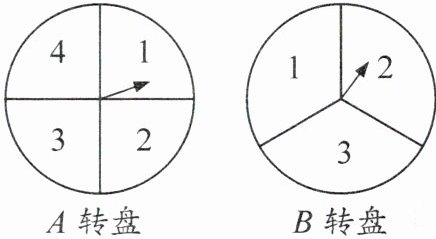
典例2 新素养 应用意识 甲与乙一起设计了一个游戏:如图是$A$,$B$两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,同时转动两个转盘,转盘停止后,若两个指针指向的数字之积小于4,则甲胜,否则乙胜(指针指向分界线时重转). 这个游戏对双方是否公平?请说明理由. 如果该游戏对双方不公平,请你设计一种对双方公平的游戏规则.


答案:这个游戏对双方不公平,理由及修改后的规则如下:
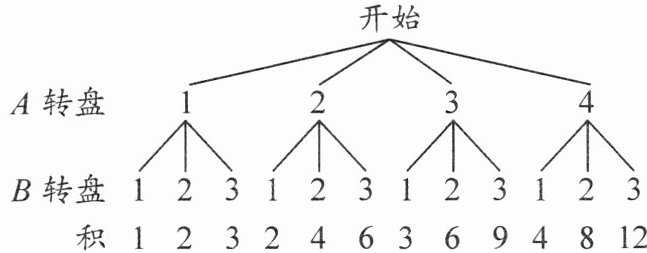
画树状图:
A转盘指针指向的数字有4种情况(1, 2, 3, 4),对应B转盘指针指向的数字均为3种情况(1, 2, 3)。
共有 $4 × 3 = 12$ 种等可能结果,分别是:
$1 × 1 = 1, 1 × 2 = 2, 1 × 3 = 3$,
$2 × 1 = 2, 2 × 2 = 4, 2 × 3 = 6$,
$3 × 1 = 3, 3 × 2 = 6, 3 × 3 = 9$,
$4 × 1 = 4, 4 × 2 = 8, 4 × 3 = 12$。
其中积小于4的结果有5种,不小于4的结果有7种。
计算概率:
甲胜的概率 $P(甲胜) = \frac{5}{12}$,
乙胜的概率 $P(乙胜) = \frac{7}{12}$。
由于 $P(甲胜) \neq P(乙胜)$,游戏对双方不公平。
修改规则:
若两个指针指向的数字之积小于4,则甲胜;
若两个指针指向的数字之积大于4,则乙胜。
画树状图:
A转盘指针指向的数字有4种情况(1, 2, 3, 4),对应B转盘指针指向的数字均为3种情况(1, 2, 3)。
共有 $4 × 3 = 12$ 种等可能结果,分别是:
$1 × 1 = 1, 1 × 2 = 2, 1 × 3 = 3$,
$2 × 1 = 2, 2 × 2 = 4, 2 × 3 = 6$,
$3 × 1 = 3, 3 × 2 = 6, 3 × 3 = 9$,
$4 × 1 = 4, 4 × 2 = 8, 4 × 3 = 12$。
其中积小于4的结果有5种,不小于4的结果有7种。
计算概率:
甲胜的概率 $P(甲胜) = \frac{5}{12}$,
乙胜的概率 $P(乙胜) = \frac{7}{12}$。
由于 $P(甲胜) \neq P(乙胜)$,游戏对双方不公平。
修改规则:
若两个指针指向的数字之积小于4,则甲胜;
若两个指针指向的数字之积大于4,则乙胜。
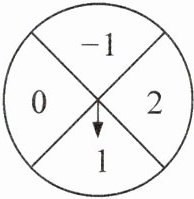
【变式2】(2025·江苏连云港模拟)如图,小颖制作了一个质地均匀且可以自由转动的转盘,转盘被等分为四个扇形,上面分别标有数字$-1$,0,1,2. 小轩、小亮用该转盘做游戏. 小轩先转动一次转盘,停止后记录下指针所指数字作为平面直角坐标系中点$H$的横坐标,然后小亮转动一次转盘,停止后记录下指针所指数字作为点$H$的纵坐标. 若点$H$恰好落在第二象限或第四象限,则小轩胜;否则小亮胜. 判断该游戏对双方是否公平,并说明理由. 如果该游戏对双方不公平,请你设计一种对双方公平的游戏规则.

答案:
【变式2】这个游戏对双方不公平. 理由如下:列表
如下:
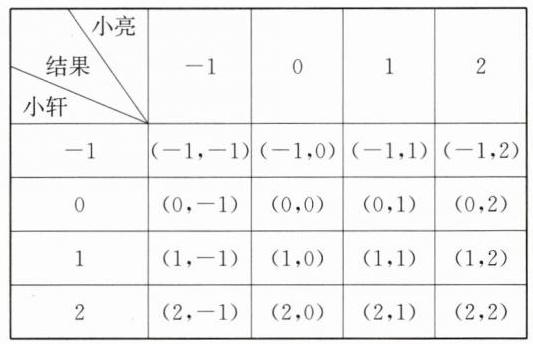
由表格可知,共有16种等可能的结果,其中点H恰好落在第二象限或第四象限的结果有4种,其他结果有12种,所以P(小轩胜$)=\frac{4}{16}=\frac{1}{4},$P(小亮胜$)=\frac{12}{16}=\frac{3}{4}. $因为P(小轩胜$)\neq P($小亮胜),所以该游戏对双方不公平. 设计游戏规则不唯一,如:若点H恰好落在第二象限或第四象限,则小轩得3分,否则小亮得1分,得分高者获胜.
【变式2】这个游戏对双方不公平. 理由如下:列表
如下:

由表格可知,共有16种等可能的结果,其中点H恰好落在第二象限或第四象限的结果有4种,其他结果有12种,所以P(小轩胜$)=\frac{4}{16}=\frac{1}{4},$P(小亮胜$)=\frac{12}{16}=\frac{3}{4}. $因为P(小轩胜$)\neq P($小亮胜),所以该游戏对双方不公平. 设计游戏规则不唯一,如:若点H恰好落在第二象限或第四象限,则小轩得3分,否则小亮得1分,得分高者获胜.