1. 下列描述不属于定义的是 (
A.单项式和多项式统称整式
B.有公共端点的两条射线组成的图形叫作角
C.两点之间线段最短
D.含有未知数的等式叫作方程
C
)A.单项式和多项式统称整式
B.有公共端点的两条射线组成的图形叫作角
C.两点之间线段最短
D.含有未知数的等式叫作方程
答案:1.C
2. 有下列语句:① 规定了原点、单位长度和正方向的直线叫作数轴;② 等式$(a + b)^2 = a^2 + 2ab + b^2$称为两数和的平方公式;③ 如果$a$,$b$为有理数,那么$(a - b)^2 = a^2 - 2ab + b^2$;④ 三角形的内角和等于$180^{\circ}$.其中,属于定义的是
①②
(填序号).答案:2.①②
3. 回忆并写出下列概念的定义:
(1)平移;
(2)旋转;
(3)轴对称;
(4)中心对称.
(1)平移;
(2)旋转;
(3)轴对称;
(4)中心对称.
答案:3.(1)一般地,在平面内,将一个图形沿直线的某个方向平行移动一定的距离后得到另一个图形的平面变换叫作平移 (2)一般地,在平面内,把一个图形绕一个定点按某个方向转动一定角度得到另一个图形的平面变换叫作旋转 (3)一般地,将一个平面图形沿某条直线翻折后得到另一个图形的平面变换叫作轴对称 (4)一般地,在平面内,若一个图形是由另一个图形绕某个点旋转180°得到的,则称这两个图形成中心对称
4. 画示意图表示下列概念之间的关系:方程、等式、一元一次方程、二元一次方程.
答案:
4.如图所示
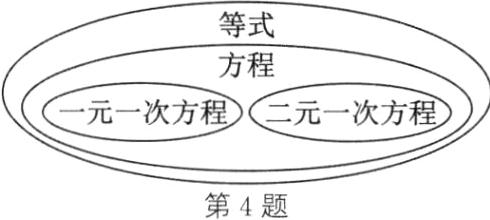
4.如图所示

5. 数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题,比如$\vert x_1 - x_2\vert$表示在数轴上数$x_1$,$x_2$对应的点之间的距离.现定义一种“$F$运算”,对于若干个数,先将每两个数作差,再将这些差的绝对值进行求和.例如:对$-1$,$1$,$2$进行“$F$运算”,得$\vert -1 - 1\vert + \vert -1 - 2\vert + \vert 1 - 2\vert = 6$.有下列说法:① 对$1$,$-2$,$3$进行“$F$运算”的结果是$10$;② 若$2 < x < y$,对$2$,$x$,$y$进行“$F$运算”的结果是$8$,则$y$的值是$8$;③ 对$a$,$a$,$b$,$c$进行“$F$运算”,化简的结果可能存在$6$种不同的表达式.其中,正确的是
①③
(填序号).答案:5.①③ 解析:由题意知,$|1-(-2)|+|1-3|+|-2-3|=3+2+5=10$,所以对1,-2,3进行“F运算”的结果是10.故①正确.由题意知,$|2-x|+|2-y|+|x-y|=-2+x-2+y-x+y=8$,解得$y=6$,故②错误.由题意知,$|a-a|+|a-b|+|a-c|+|a-b|+|a-c|+|b-c|=2|a-b|+2|a-c|+|b-c|$,当$a-b \geqslant 0,a-c \geqslant 0,b-c \geqslant 0$时,$2|a-b|+2|a-c|+|b-c|=2a-2b+2a-2c+b-c=4a-b-3c$;当$a-b \geqslant 0,a-c \geqslant 0,b-c \leqslant 0$时,$2|a-b|+2|a-c|+|b-c|=2a-2b+2a-2c-b+c=4a-3b-c$;当$a-b \leqslant 0,a-c \geqslant 0,b-c \geqslant 0$时,$2|a-b|+2|a-c|+|b-c|=-2a+2b+2a-2c+b-c=3b-3c$;当$a-b \geqslant 0,a-c \leqslant 0,b-c \leqslant 0$时,$2|a-b|+2|a-c|+|b-c|=2a-2b-2a+2c-b+c=-3b+3c$;当$a-b \leqslant 0,a-c \leqslant 0,b-c \geqslant 0$时,$2|a-b|+2|a-c|+|b-c|=-2a+2b-2a+2c+b-c=-4a+3b+c$;当$a-b \leqslant 0,a-c \leqslant 0,b-c \leqslant 0$时,$2|a-b|+2|a-c|+|b-c|=-2a+2b-2a+2c-b+c=-4a+b+3c$.所以可能有6种不同的表达式.故③正确.综上所述,正确的是①③.
解析:
①对1,-2,3进行“F运算”:$|1 - (-2)| + |1 - 3| + |-2 - 3| = 3 + 2 + 5 = 10$,故①正确.
②对2,x,y($2 < x < y$)进行“F运算”:$|2 - x| + |2 - y| + |x - y| = (x - 2) + (y - 2) + (y - x) = 2y - 4$,由$2y - 4 = 8$,解得$y = 6$,故②错误.
③对a,a,b,c进行“F运算”:$|a - a| + |a - b| + |a - c| + |a - b| + |a - c| + |b - c| = 2|a - b| + 2|a - c| + |b - c|$.
当$a \geq b \geq c$时,$2(a - b) + 2(a - c) + (b - c) = 4a - b - 3c$;
当$a \geq c \geq b$时,$2(a - b) + 2(a - c) + (c - b) = 4a - 3b - c$;
当$b \geq a \geq c$时,$2(b - a) + 2(a - c) + (b - c) = 3b - 3c$;
当$c \geq a \geq b$时,$2(a - b) + 2(c - a) + (c - b) = -3b + 3c$;
当$b \geq c \geq a$时,$2(b - a) + 2(c - a) + (b - c) = -4a + 3b + c$;
当$c \geq b \geq a$时,$2(b - a) + 2(c - a) + (c - b) = -4a + b + 3c$,共6种不同表达式,故③正确.
正确的是①③.
②对2,x,y($2 < x < y$)进行“F运算”:$|2 - x| + |2 - y| + |x - y| = (x - 2) + (y - 2) + (y - x) = 2y - 4$,由$2y - 4 = 8$,解得$y = 6$,故②错误.
③对a,a,b,c进行“F运算”:$|a - a| + |a - b| + |a - c| + |a - b| + |a - c| + |b - c| = 2|a - b| + 2|a - c| + |b - c|$.
当$a \geq b \geq c$时,$2(a - b) + 2(a - c) + (b - c) = 4a - b - 3c$;
当$a \geq c \geq b$时,$2(a - b) + 2(a - c) + (c - b) = 4a - 3b - c$;
当$b \geq a \geq c$时,$2(b - a) + 2(a - c) + (b - c) = 3b - 3c$;
当$c \geq a \geq b$时,$2(a - b) + 2(c - a) + (c - b) = -3b + 3c$;
当$b \geq c \geq a$时,$2(b - a) + 2(c - a) + (b - c) = -4a + 3b + c$;
当$c \geq b \geq a$时,$2(b - a) + 2(c - a) + (c - b) = -4a + b + 3c$,共6种不同表达式,故③正确.
正确的是①③.