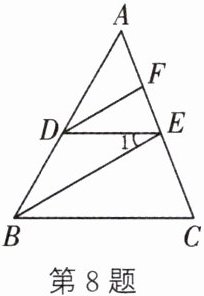
8. 如图,∠ADE = 60°,DF 平分∠ADE,∠1 = 30°。求证:DF//BE。
证明:∵ DF 平分∠ADE,∠ADE = 60°(已知),
∴
∵ ∠1 = 30°(已知),
∴
∴
证明:∵ DF 平分∠ADE,∠ADE = 60°(已知),
∴
∠FDE
= $\frac{1}{2}$∠ADE = 30°(角的平分线的定义
)。∵ ∠1 = 30°(已知),
∴
∠FDE
= ∠1
(等量代换
),∴
DF//BE
(内错角相等,两直线平行
)。
答案:8. ∠FDE 角的平分线的定义 ∠FDE ∠1 等量代换 DF//BE 内错角相等,两直线平行
解析:
证明:
∵ DF 平分∠ADE,∠ADE = 60°(已知),
∴∠FDE = $\frac{1}{2}$∠ADE = 30°(角的平分线的定义)。
∵ ∠1 = 30°(已知),
∴∠FDE = ∠1(等量代换),
∴DF//BE(内错角相等,两直线平行)。
∵ DF 平分∠ADE,∠ADE = 60°(已知),
∴∠FDE = $\frac{1}{2}$∠ADE = 30°(角的平分线的定义)。
∵ ∠1 = 30°(已知),
∴∠FDE = ∠1(等量代换),
∴DF//BE(内错角相等,两直线平行)。
9. 求证:三个连续自然数之和能被 3 整除。
答案:9. 设三个连续自然数为 $a, a + 1, a + 2$,其中 $a$ 为自然数,则 $a + (a + 1) + (a + 2) = a + a + 1 + a + 2 = 3a + 3 = 3(a + 1)$。
∵ $a + 1$ 为自然数,
∴ $3(a + 1)$ 能被 3 整除,
∴ 三个连续自然数之和能被 3 整除
∵ $a + 1$ 为自然数,
∴ $3(a + 1)$ 能被 3 整除,
∴ 三个连续自然数之和能被 3 整除
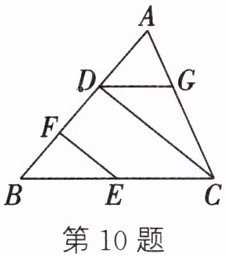
10. (新考法·条件开放题)图形的世界丰富且充满变化,用数学的眼光观察它们,奇妙无比。如图,EF//CD,请根据图形特征添加一个关于角的条件,使得∠BEF = ∠CDG,并给出证明过程。

答案:10. 答案不唯一,如添加的条件:∠B + ∠BDG = 180° 证明:
∵ EF//CD(已知),
∴ ∠BEF = ∠BCD(两直线平行,同位角相等)。
∵ ∠B + ∠BDG = 180°(已知),
∴ BC//DG(同旁内角互补,两直线平行),
∴ ∠CDG = ∠BCD(两直线平行,内错角相等),
∴ ∠BEF = ∠CDG(等量代换)
∵ EF//CD(已知),
∴ ∠BEF = ∠BCD(两直线平行,同位角相等)。
∵ ∠B + ∠BDG = 180°(已知),
∴ BC//DG(同旁内角互补,两直线平行),
∴ ∠CDG = ∠BCD(两直线平行,内错角相等),
∴ ∠BEF = ∠CDG(等量代换)
11. 在整数除法体系中,一个正整数除以 3 的余数规律蕴含着深刻的数学逻辑。我们把一个正整数 a 除以 3 所得的余数记作“a 模 3”,例如:12÷3 = 4……0 记作“12 模 3 = 0”;16÷3 = 5……1 记作“16 模 3 = 1”;11÷3 = 3……2 记作“11 模 3 = 2”。
(1)直接写出结果:36 模 3 =
(2)命题:如果 a 模 3 = 1,其中 a 为正整数,那么 10a 模 3 = 1。判断该命题是否为真命题。若是,请写出证明过程;若不是,请举例说明。
(3)证明:如果 a 模 3 = 1,b 模 3 = 2,其中 a,b 为正整数,那么(a + b)模 3 = 0。
(1)直接写出结果:36 模 3 =
0
;360 模 3 =0
。(2)命题:如果 a 模 3 = 1,其中 a 为正整数,那么 10a 模 3 = 1。判断该命题是否为真命题。若是,请写出证明过程;若不是,请举例说明。
(3)证明:如果 a 模 3 = 1,b 模 3 = 2,其中 a,b 为正整数,那么(a + b)模 3 = 0。
答案:11. (1) 0 0 (2) 是真命题
∵ $a$ 模 3 = 1,其中 $a$ 为正整数,
∴ $a$ 除以 3 余 1,可以设 $a = 3k + 1$,$k$ 为自然数,则 $10a = 10(3k + 1) = 30k + 10$。
∵ 30k 能被 3 整除,10 除以 3 余 1,
∴ $(30k + 10)$ 模 3 = 1,即 $10a$ 模 3 = 1 (3)
∵ $a$ 模 3 = 1,$b$ 模 3 = 2,
∴ 设 $a = 3n + 1$,$b = 3m + 2$,$m,n$ 是自然数,
∴ $a + b = 3n + 1 + 3m + 2 = 3n + 3m + 3 = 3(n + m + 1)$,
∴ $3(n + m + 1)$ 模 3 = 0,即 $(a + b)$ 模 3 = 0
∵ $a$ 模 3 = 1,其中 $a$ 为正整数,
∴ $a$ 除以 3 余 1,可以设 $a = 3k + 1$,$k$ 为自然数,则 $10a = 10(3k + 1) = 30k + 10$。
∵ 30k 能被 3 整除,10 除以 3 余 1,
∴ $(30k + 10)$ 模 3 = 1,即 $10a$ 模 3 = 1 (3)
∵ $a$ 模 3 = 1,$b$ 模 3 = 2,
∴ 设 $a = 3n + 1$,$b = 3m + 2$,$m,n$ 是自然数,
∴ $a + b = 3n + 1 + 3m + 2 = 3n + 3m + 3 = 3(n + m + 1)$,
∴ $3(n + m + 1)$ 模 3 = 0,即 $(a + b)$ 模 3 = 0